هندسة التحكم ، هي مجال متعدد التخصصات تصل جذوره إلى هندسة الرياضيات التطبيقية . الهدف الأساسي لهندسة التحكم هو تصميم أنظمة تستجيب لأي مُدخلات بطريقة متوقعة و مرغوب بها و لذلك الحاجة لأجهزة التحكم بديهية فإن لم نتمكن من جعل النظام يتصرف بطريقة مرغوب بها فلن يكون نظام مفيد و الأسوء أنه قد يكون نظام خطير.

نظريات التحكم لها إستخدمات واسعة من إدارة الشبكات المرورية إلى التنبؤ بتصرفات الحيوانات مروراً بأنظمة النماذج النفسية. نظريا كل عضو في النظام البيولوجي في الجسم يستخدم شكل من أشكال التحكم ، كدرحة حرارة الجسم ضغط الدم ، السكر إلخ. و حتى العضلات الهيكلية تعتمد في رده فعلها على ما يسمى بنظام التحكم ذا التغذية الرجعية كمثال لو جلسنا في غرفة ساخنة لفترة طويلة ستزداد حرارة أجسامنا و بالتالي ستقوم المستقبلات الحرارية في بشرتنا بإلتقاط هذا التغير في الحرارة و إرسال إشارات تحذيرية لجزء من الدماغ يدعى الغده النخامية و التي بدورها ترسل إشارات إلى الغدد العرقيه كي تبدأ بالعمل و هذا ما يساعد في إرجاع درحة حرارة أجسامتا للوضع الطبيعي.

كما أن أنظمة التحكم لها أهمية بالغة في الروبوتات حيث تستخدم لتنفيذ أوامر الحركه كالقيادة حول مسار معين أو المحافظة على سرعة معينه ، و أحد أكثر أجهزة التحكم شيوعاً هو متحكم البيد (PID controller)

و أحد السبل لتقسيم نظريات التحكم إلى جزئين هي بمقارنه نظام التحكم مفتوح العقده (open loop control) بنظام التحكم مغلق العقده (closed loop control) و الذي يسمى كذلك بنظام التحكم ذا تغذية رجعية (feedback control) .

أنظمة التحكم المفتوحة العقدة

أنظمة التحكم المفتوحة العقدة يسهل تصورها فنحن نعطي النظام مُدخل (input) و ينتج عن ذلك مُخرج ما (output) من دون أي محاولة لحساب ما إذا كان المُخرج هو الإستجابة المطلوبة للنظام . و مثال على الأنظمة المفتوحة العقدة هي الغسلات ، فهي تعتمد على مؤقت و ليس على مدى نظافة الملابس.

و الرسم المستخدم لوصف أنظمة التحكم يسمى بمخطط القوالب (block diagram) حيث من التقليدي أن يرمز للمُدخل بـ (u(t)) و أن يرمز للإستجابة بـ(y(t)) بينما النظام الذي يتم التحكم فيه يسمى بالمنشأه (plant) . نلاحظ أن كل من المدخلات و المخرجات هم دوال بالنسبة للزمن .

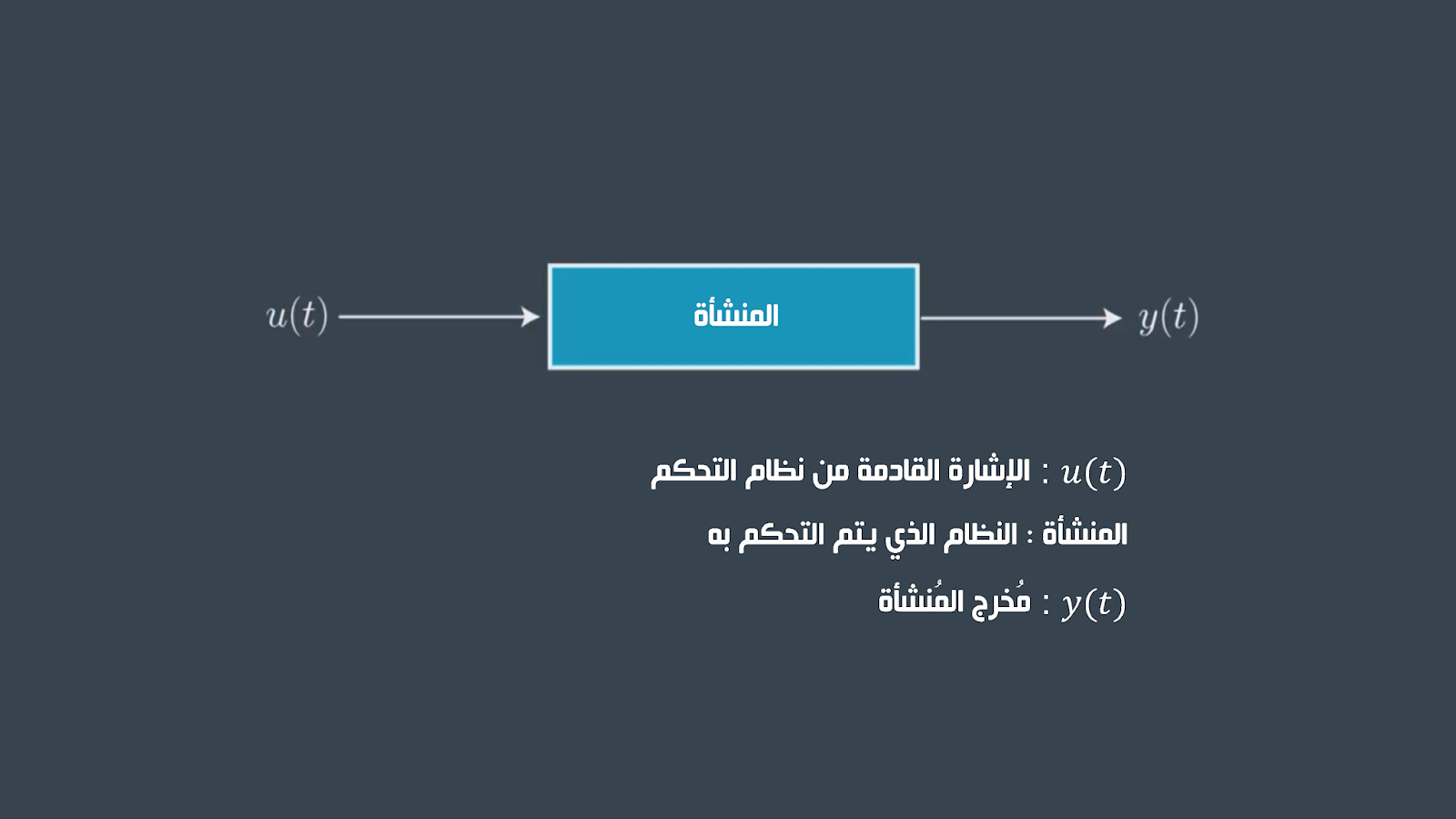
كما نرى فالمتحكمات مفتوحة العقدة مفيدة جداُ في حال أن نسبة التبنؤ بمخرجات النظام كانت عالية و كان النظام بشكل عام أمن و ذلك لأن المدخلات في النظام ليس مقدورها معرفة ما إذا كان المخرج هو الإستجابة المرغوبة لدينا .

أنظمة التحكم المغلقة العقدة

في الأنطمة المغلقة العقدة سنقوم بإستخدام حساسات لمراقبة المُخرج ، و من ثم سنقوم بربط قراءات الحساسات بالمدخل ، وبهذا بوسعنا تغيير المُدخل بناءً على قراءات المُخرج ولهذا يطلق على هذه الأنظمة كذلك بأنظمة التحكم ذا تغذية رجعية . و توصف هذه التغذية الرجعية بالرمز (y(t)) لأنه تحت الظروف المثالية فإن الحساسات تقوم بقياس مخرجات النظام بشكل دقيق. وإذا قمنا بطرح قيمة (y(t)) من المدخلات عن طريق إستخدام عقدة تجميع فالفرق هو معامل الخطأ (e(t)) . و للتعامل مع الخطأ فسنقوم بإيصاله بمتحكم و بدوره سيقوم المتحكم بإنتاج قيمة جديدة تُدخل على المنشأه أو النظام لدينا و هذا المُدخل الجديد يرمز له (u(t)) بينما المدخل الذي نمده للنظام يطلق عليه الإشارة المرجعية ورمزه (r(t)) . وهذه الصورة توضح رسم هذا النظام

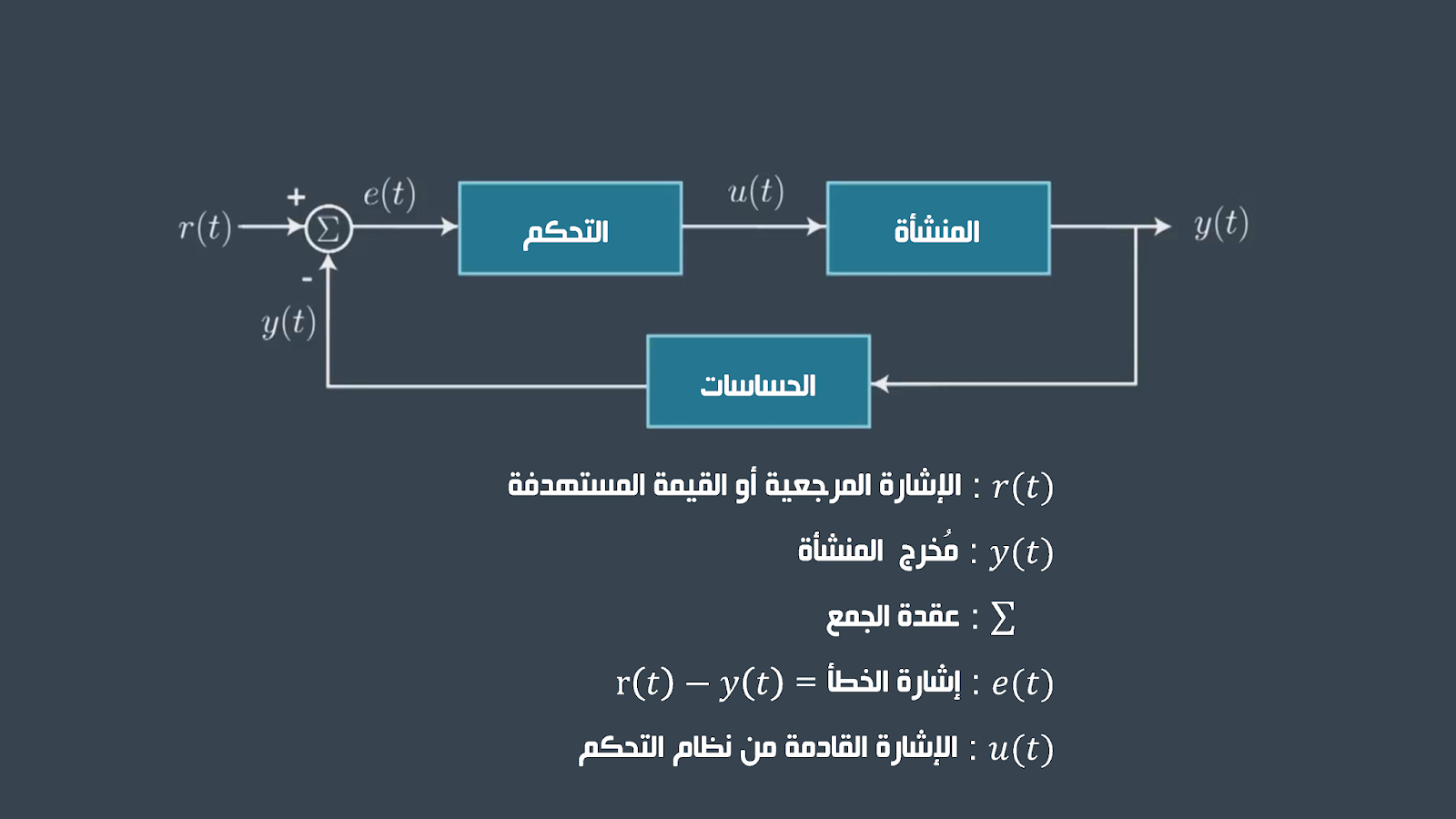
حتى الأن تعرفنا على الفرق الرئيسي بين المتحكمات مفتوحة العقدة و مغلقة العقدة و الفوائد التي توفرها لنا المتحكمات ذات التغذية الرجعية . و الأن سنتعرف على طريقة عمل هذه المتحكمات.

التحكم التناسبي التكاملي التفاضلي

أحد أشهر أنظمة التحكم هو نظام التحكم التناسبي التكاملي التفاضلي (proportional integral and derivative controller) أو بإختصار متحكم البيد (PID controller) و أحيانا يعرف هذا النظام بالمتحكم ذو االعُقد الثلاثة . و سبب شهرته هو إثباته لنجاحه في الكثير من التطبيقات لمختلف المجالات الميكانيكيه و الكهربائية و حتى التطبيقات الكيميائية . وما يميز متحكم البيد هو رخص تصنيعه و سهولة إستخدامه حيث لا يتطلب فهم للنموذج الرياضي (mathematical model) للعملية المراد التحكم بها.

لكن أنظمة تحكم البيد هي مجال واسع و هناك العديد من الأنواع المختلفة و في هذا المقال سنركز فقط على أبسط الأنواع أو ما يعرف بمتحكم البيد المثالي.

متحكم البيد يقوم بحساب قيمة الخطأ كالفرق بين القيمة المحسوبة (process variable) و القيمة المستهدفة (setpoint) و ذلك يتم عن طريق ضبط معايير معينة و خوارزمية متحكم البيد تتضمن ثلاثة معايير متفرقة و أحيانا تسمى حدود التحكم الثلاث و هم :

التناسب (kp)
التكامل (ki)
التفاضل (kd)

هولاء هم العُقد الثلاثة التي يجب ضبطها من قبل مصصم المتحكم ، و مخرج المتحكم (Controller output) هو المجموع الجبري للمعايير الثلاثة

$u(t)=K_{p} e(t)+K_{i} \int_{0}^{t} e(\tau) d \tau+K_{d} \frac{d e(t)}{d t}$

بعض التطبيقات قد تطلب إستخدام معييار أو معييارين من معايير متحكم البيد ، و يمكن القيام بهذا عن طريق تصفير بقية المعايير. وفي حالة مثل هذه يسمى متحكم P أو i أو D أو PD أو PI . في الواقع معظم متحكمات البيد هي في الأصل متحكم PI

المحاكاة :

لنتعرف أكثر على تأثير كل معيار من معايير البيد الثلاثة سنقوم بتطبيقها على محاكاة مبسطة لطائرة رباعية (1d quadrotor) ،

الهدف من المحاكاه هو جعل الطائرة تحلق من الأرض إلى إرتفاع عشرة أمتار و تحافظ على هذا الإرتفاع ، وبالتالي سينتج لنا ثلاثة رسوم بيانية :

الأول : يصف زمن الوصول إلى الإرتفاع المطلوب

الثاني : يصف سرعة الطائرة نسبة للزمن

الثالث : يصف جهد التحكم بالنسبة للزمن ، و جهد التحكم يعرف بأنه مقدار الجهد الذي تبذله الطائرة لتصل إلى هدفها المحدد.

برمجة المحاكي نفسها ستكون مقسمة إلى ثلاثة أقسام.

القسم الأول : و يصف معادلات الحركة بالنسبة للطائرة الرباعية .
القسم الثاني : يصف نوع المتحكم
القسم الثالث : حيث نجري المحاكاة .

متحكم التناسب :

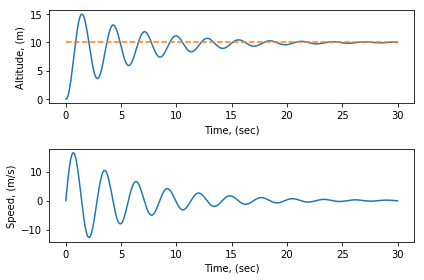
يعتبر من أسهل أنواع المتحكمات ، ولنفترض بأن الطائره لها حساس بمقدوره حساب إرتفاعها . في البداية الطائرة في وضع الإستعداد على الأرض و بعد تفعيلها يقوم مسار الطيران المبرمج فيها بجعلها تحلق لإرتفاع عشرة أمتار ومن ثم المحافظة على هذا الإرتفاع لمدة خمسة ثواني ، ومن ثم الطيران لأي تجاه محافظة على نفس اللإرتفاع .

في اللحظة الأولى التي تقوم بها الطائرة بتنفيذ مسار الطيران ، فخطأ الإرتفاع كالأتي :

$\begin{aligned} e(t) &=r-y(t) \\ &=10 m-0 \\ &=10 m \end{aligned}$

فبالتالي يقوم المتحكم بالشعور بهذا الخطأ ومن ثم يأمر المحركات بإنتاج قوة دفع عامودية متناسبة (proportional) مع الخطأ كالأتي :

$u(t)=K_{p} * e(t)$

و بالتالي كلما إرتفعت الطائرة قل الخطأ و قل مُدخل (input) المتحكم

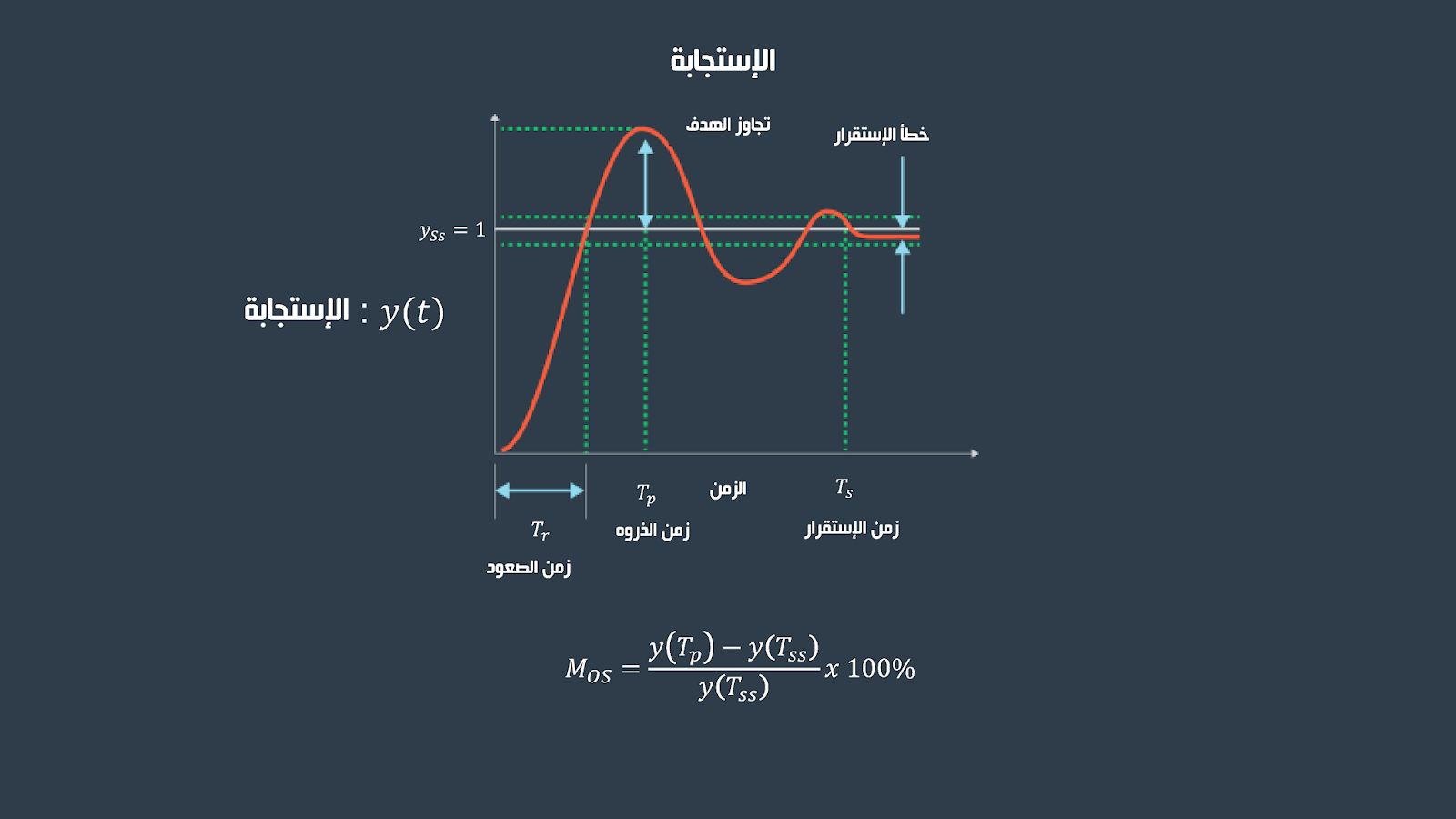
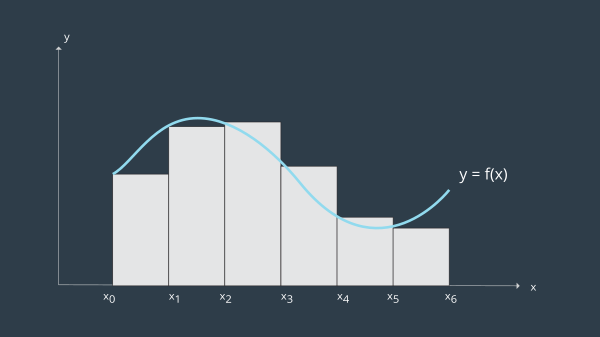
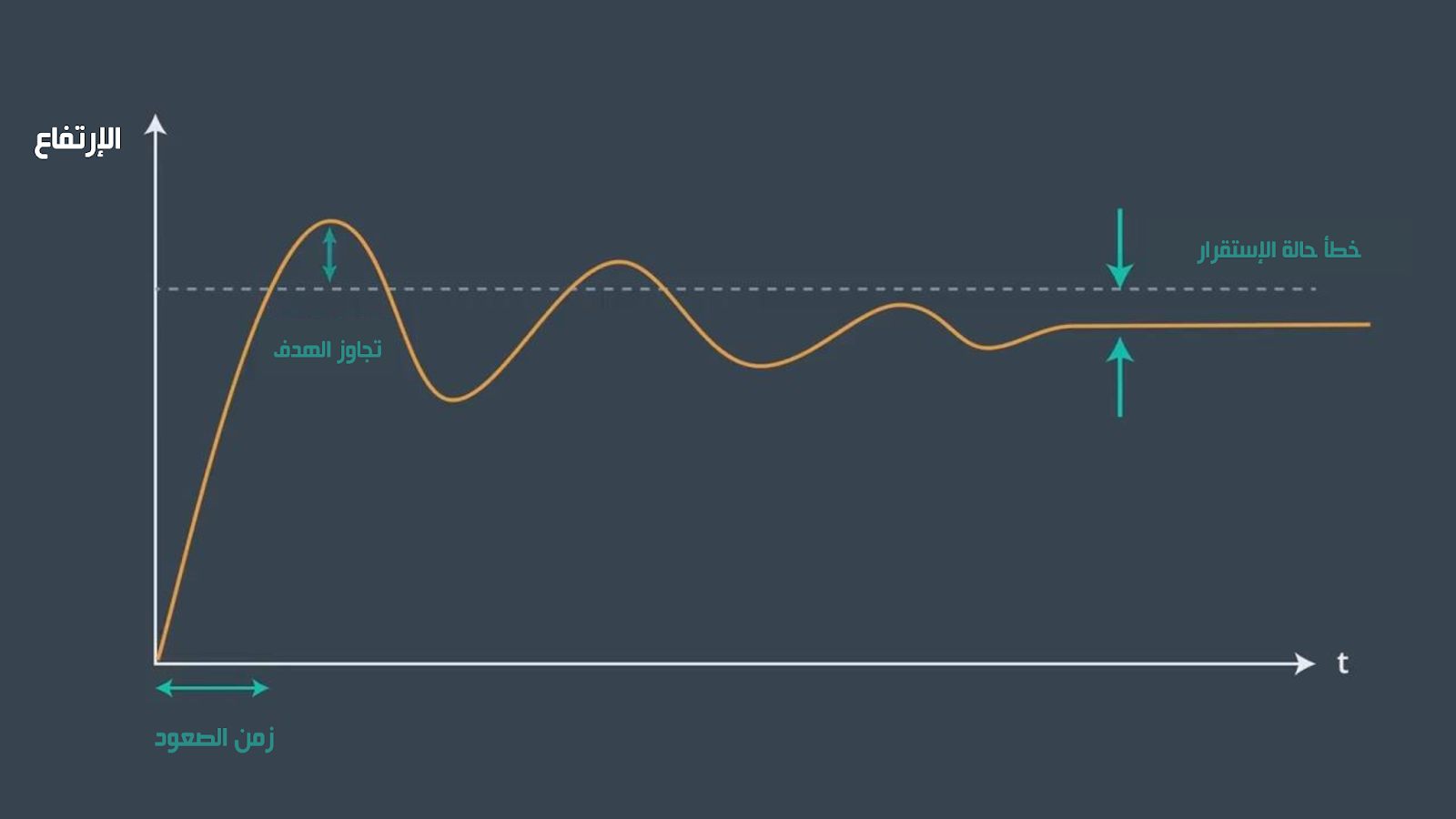
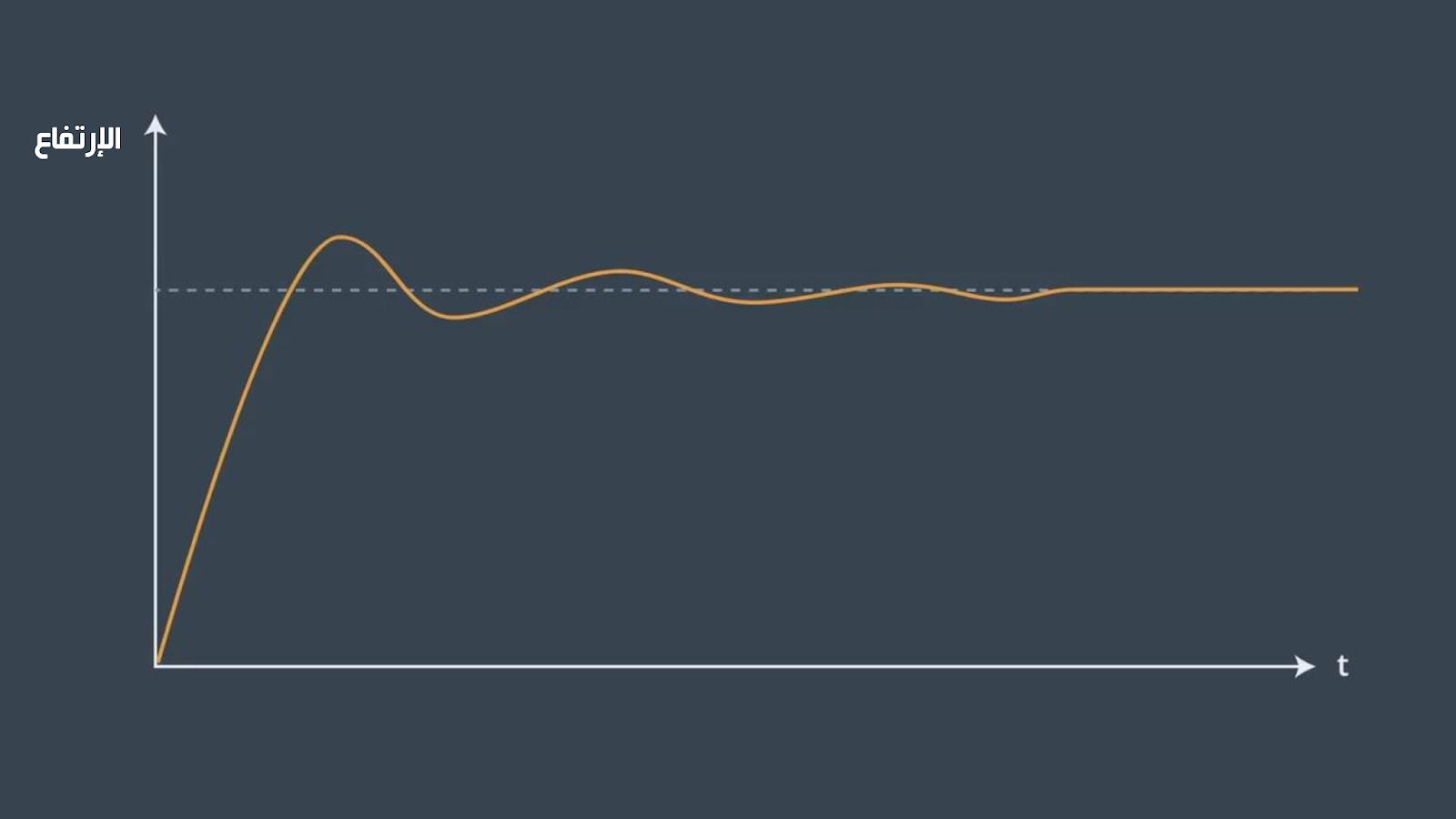
الكثير من الأنظمة في حياتنا اليوم تحكمها معادلات تفاضلية من الدرجة الثانية (second-order differential equations) وهي معرضة للإضطرابات و الذبذبات عند الإستجابة لأي تغير قبل أن تصل إلى حالة إستقرار . و حالة التذبذب التي تمر بها هذه الأنطمة موضحة في الصورة الأتيه

زمن الصعود (Rise time) : هو وقت الإستجابة المطلوب للتحرك من قيمة منخفضة إلى قيمة عالية ، وفي الغالي يوصف كنسبة مئوية

زمن الذروه (Peak time) : هو الوقت المطلوب للوصول لأول نقطة تجاوز الهدف (overshoot)
القيمة القصوى لتجاوز الهدف تعطى بالمعادلة

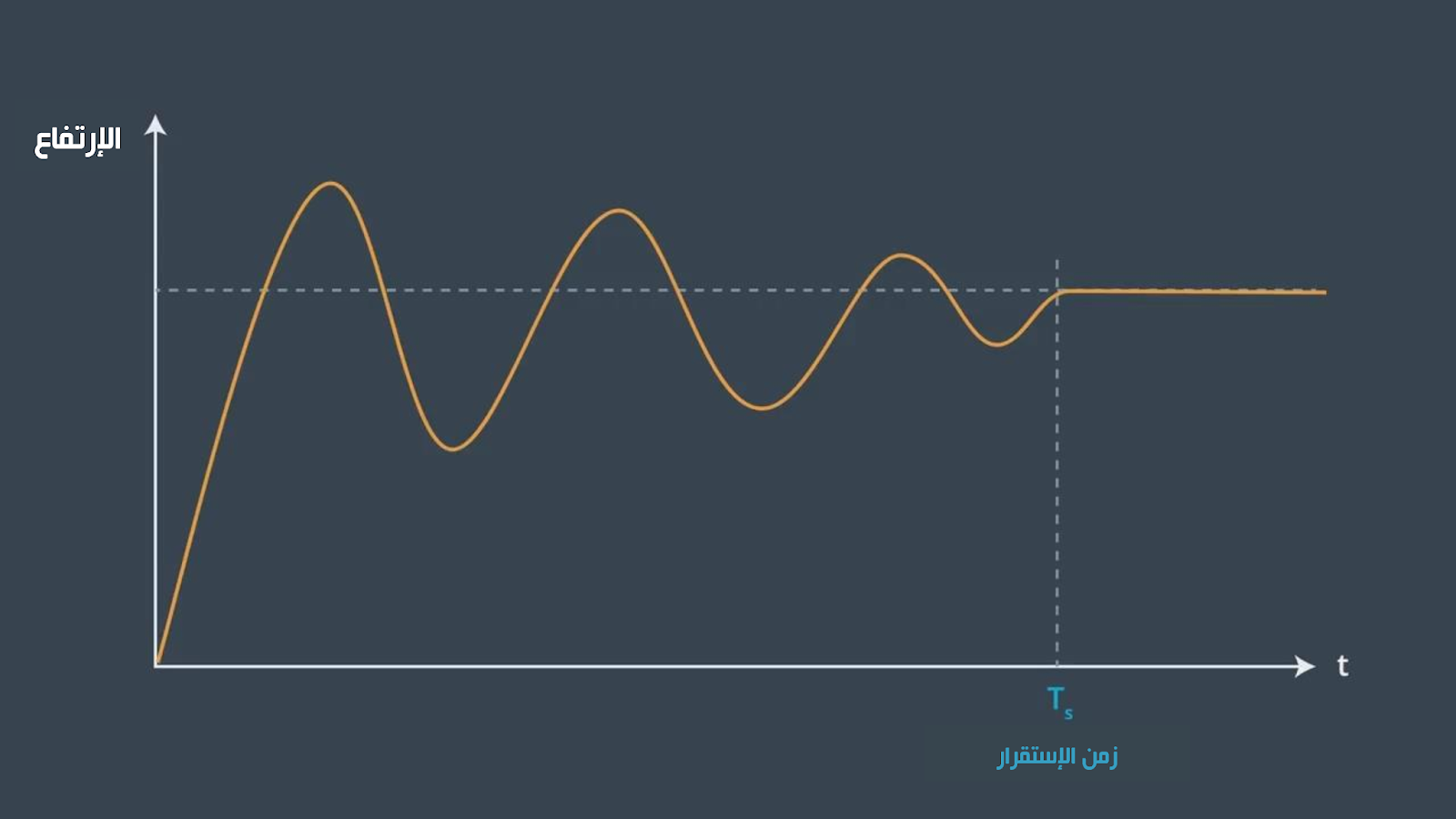
$M_{O S}=\frac{y\left(T_{p}\right)-y\left(T_{s s}\right)}{y\left(T_{s s}\right)} \times 100 \%$

زمن الإستقرار (Settling time) : و هو وقت الإستجابة المطلوب للوصول و البقاء في نطاق محدد قريب من قيمة حالة الإستقرار (steady-state)

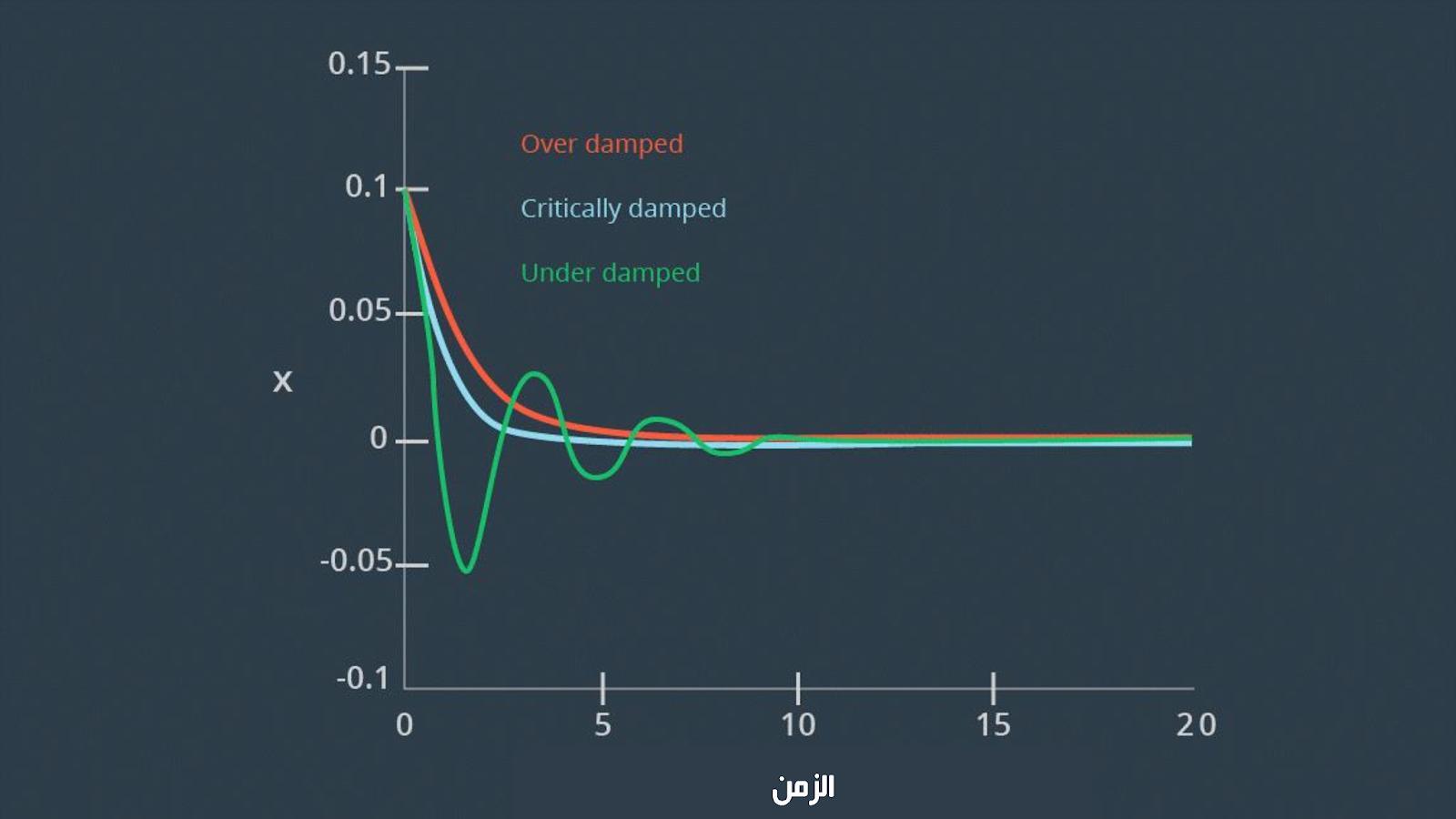
التذبذب مربوط بشكل كبير بكمية التخميد (damping) التي يحتويها النظام ، والصورة التالي توضح الأنواع الثلاثة للتخميد

و لبرمجة هذا المتحكم في المحاكاة نقوم بالأتي

معادلات حركة الطائرة

#  نفس الكود السابق

متحكم التناسب والتكامل

class PI_Controller:
    def __init__(self, kp = 0.0, ki = 0.0, start_time = 0):
        
        # إستهلال القيمة الأوليه لمعامل متحكم التناسب
        # ومعامل متحكم التفاضل
        self.kp_ = float(kp)
        self.kd_ = float(kd)
        
        #إستهلال قيمة الخطأ الأخير
        self.last_error_ = 0.0
        
        # إستهلال قيمة مجموع الخطأ
        self.error_sum_ = 0.0
        
        # إستهلال القيمة المستهدفة بصفر
        self.set_point_ = 0
        # إستهلال قيمة الزمن البدائي
        self.start_time_ = start_time

        # حفظ القيمة السابقة للزمن
        self.last_timestamp_ = 0.0

        # تخزين قيم جهد التحكم
        self.u_p = [0]
        self.u_d = [0]

    # تحديد الإرتفاع المستهدف
    def setTarget(self, target):
        self.set_point_ = float(target)

    # تحديد قيمة معامل تحكم التناسب
    def setKP(self, kp):        
        self.kp_ = float(kp)
    
    # تحديد قيمة معامل تحكم التفاضل
    def setKD(self, kd):       
        self.kd_ = float(kd)

    # تحديث
    def update(self, measured_value, timestamp):
        # حساب معامل التغير في الزمن
        delta_time = timestamp - self.last_timestamp_
        
        if delta_time == 0:
            # لو كانت دلتا الوقت تساوي صفر
            return 0
        
        # حساب الخطأ كناتج الفرق بين القيمة المستهدفة
        # و القيمة المحسوبة        
        error = self.set_point_ - measured_value

        # تحديث قيمة الزمن السابق بالزمن الحالي 
        self.last_timestamp_ = timestamp
        
        # حساب مجموع الخطأ 
        self.error_sum_ += error * delta_time
        
        # حساب التغير في الخطأ
        delta_error = error - self.last_error_
        
        #تحديت الخطأ الأخير بالخطأ الحالي
        self.last_error_ = error
        
        # حساب خطأ التناسب
        p = self.kp_ * error
        
        # حساب خطأ التفاضل
        d = self.kd_ * (delta_error / delta_time)
        
        
        # تحديد جهد التحكم
        u = p + d
        
        # تخزين قيم جهد التحكم 
        self.u_p.append(p)
        self.u_d.append(d)

        return u

المحاكاة

# معامل التناسب
kp = 0.76
# ومعامل التكامل
ki = 0.10
# معايير المحاكاة
N = 500 # عدد نقاط المحاكاة
t0 = 0  # وقت البداية
tf = 30 # وقت النهاية
time = np.linspace(t0, tf, N)
dt = time[1] - time[0] # التغير في الزمن

##################
# إستهلال القيم
y = [0, 0]
   #y[0] = قيمة الإرتفاع
   #y[1] = قيمة السرعة

# إستهلال مصفوفة لتخزين القيم
soln = np.zeros((len(time),len(y)))

# قيمة متخكم التناسب
pi = PI_Controller()

# تحديد معامل التناسب
pi.setKP(kp)

# تحديد معامل التكامل
pi.setKP(kp)

# تحديد قيمة الإرتفاع
r = 10 # أمتار
pi.setTarget(r)

# محاكاة حركة الطائرة
j = 0 # عداد
for t in time:
    # جساب الحالة في النفطة التالية للزمن
    y = ydot(y,t,pi)
    # تخزين النتائج
    soln[j,:] = y
    j += 1

# رسم النتائج
SP = np.ones_like(time)*r 
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax1.plot(time, soln[:,0],time,SP,'--')
ax1.set_xlabel('Time, (sec)')
ax1.set_ylabel('Altitude, (m)')

ax2 = fig.add_subplot(212)
ax2.plot(time, soln[:,1])
ax2.set_xlabel('Time, (sec)')
ax2.set_ylabel('Speed, (m/s)')
plt.tight_layout()
plt.show()

fig2 = plt.figure()
ax3 = fig2.add_subplot(111)
ax3.plot(time, p.u_p, label='u_p', linewidth=3, color = 'red')
ax3.set_xlabel('Time, (sec)')
ax3.set_ylabel('Control Effort')
h, l = ax3.get_legend_handles_labels()
ax3.legend(h, l)
plt.tight_layout()
plt.show()
##################
y0 = soln[:,0] #الإرتفاع
rise_time_index =  np.argmax(y0&gt;r)
RT = time[rise_time_index]
print("The rise time is {0:.3f} seconds".format(RT))

OS = (np.max(y0) - r)/r*100
if OS < 0:
    OS = 0
print("The percent overshoot is {0:.1f}%".format(OS))

print ("The steady state offset at 30 seconds is {0:.3f} meters".format(abs(soln[-1,0]-r)))

الرسومات الناتجة ستكون بهذا الشكل

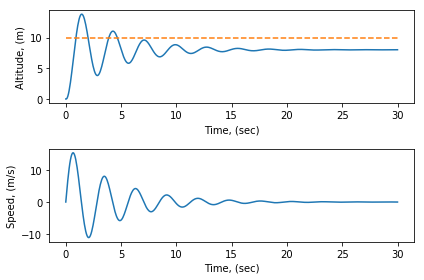
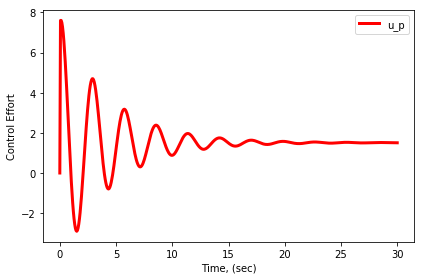
متحكم التناسب و التكامل :

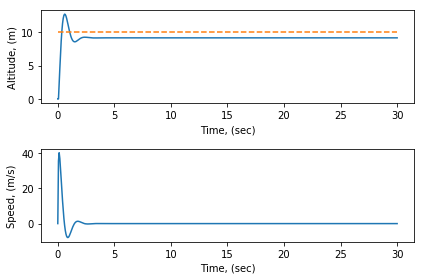
في الغالب هناك متطلبات تصميم صرمة جداً فيما يتعلق بمقدار خطأ حالة الإستقرار (steady-state error) المقبولة و لهذا متحكم التناسب لوحده غير كافي . و طريقة تقليل أو التخلص من هذا الخطأ هي بإضافة معييار التكامل .

و الفكرة ببساطة هي بزيادة مُدخل المتحكم نسبة إلى مجموع الخطأ المتراكم. فبالتالي سيأخذ مُتحكم التكامل في إعتباره كل قيم الأخطاء السابقة . و نتيجة لذلك فحتى الأخطاء الصغيرة سيتم تضخيمها مما يجعل المتحكم يزيد من القيمة المُدخله (input) للنظام . وبهذه الطريقة سيتخلص متحكم التكامل من أخطاء حالة الإستقرار الصغيرة و التي كان متحكم التناسب عرضة لها .

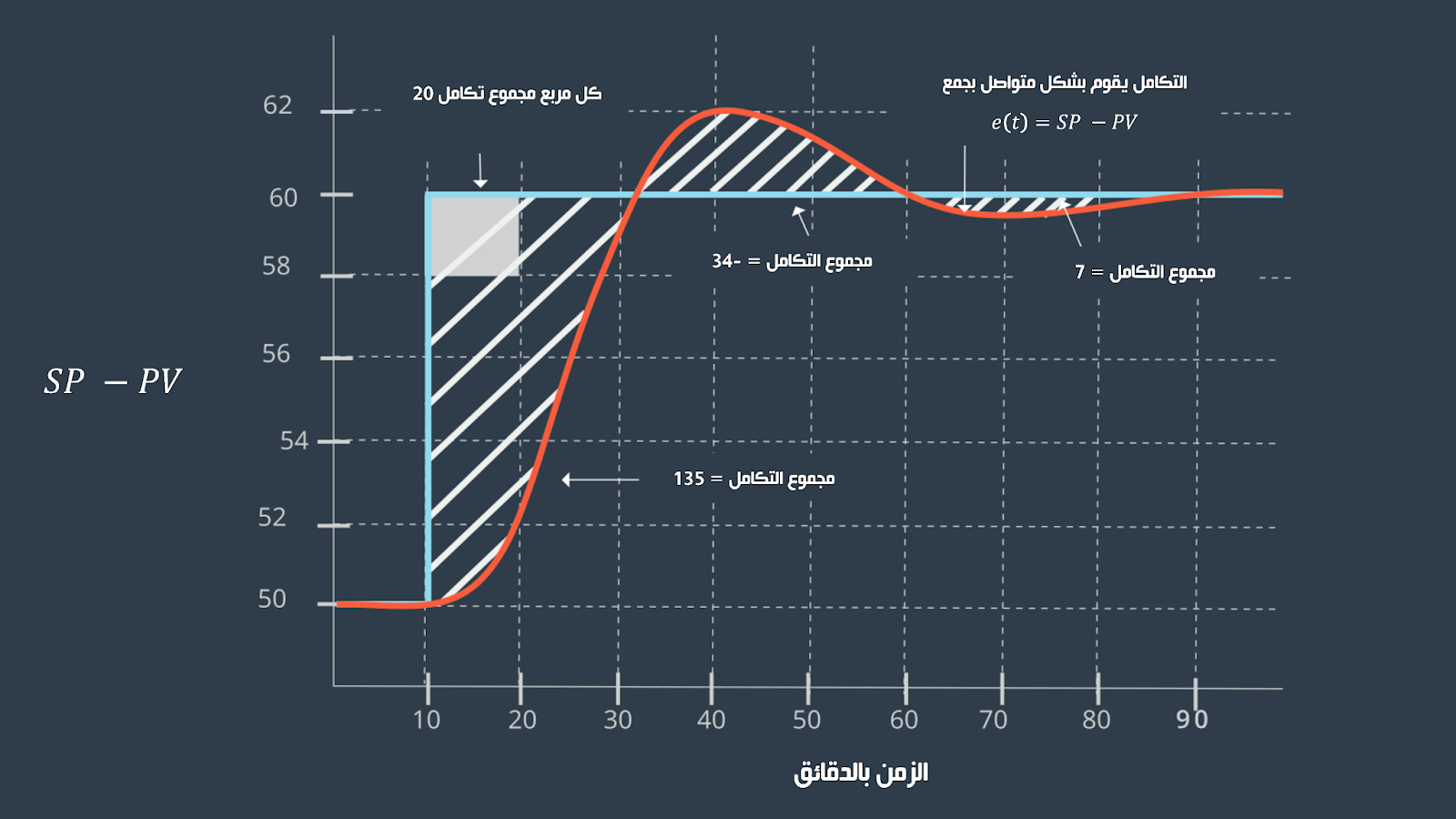
القيمة المحسوبة (PV) والقيمة المستهدفة (SP)

قد يدور في خاطر البعض كيف يتم تطبيق معادلة التحكم متواصلة الزمن (continuous time controller) على الحواسيب ، فالحواسيب هي أجهزة متقطعة الزمن (discrete-time) ، كمثال يمكننا أن نرى سيارة تغير سرعتها بشكل سلس و متواصل بينما تتسارع على الطرق بينما كما هو موضح في الصورة الأتيه

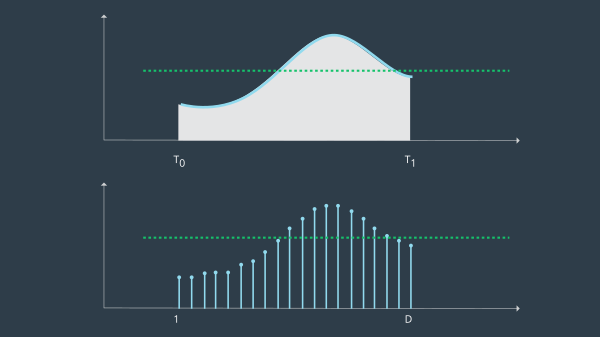
لكن الحواسب ترى فقط عينات مقطعة بشكل دوري ، و وهنا تظهر أهمية التكامل حيث يقوم بحساب المنطقة تحت المُنحنى وذلك عن طريق جمع المستطيلات بإستخدام مجموع ريمان (Riemann sum)

$\int_{0}^{t} e(\tau) d \tau \approx \sum_{k=1}^{n} e_{k} \Delta t$

إرتفاع المثلث هو الخطاً في كل نقطة زمن و العرض هو الفترة الزمنية

و بالتالي في كل خطوة زمنية جديدة () كل ما علينا هو حساب الخطأ الجديد و إضافته للمجموع

$E_{k} = E_{k-1} + e_{k}$

وهذه طريقة برمجة متحكم PI

معادلات حركة الطائرة

#  نفس الكود السابق

متحكم التناسب والتكامل

class PI_Controller:
    def __init__(self, kp = 0.0, ki = 0.0, start_time = 0):
        
        # إستهلال القيمة الأوليه لمعامل متحكم التناسب
        # ومعامل متحكم التفاضل
        self.kp_ = float(kp)
        self.kd_ = float(kd)
        
        #إستهلال قيمة الخطأ الأخير
        self.last_error_ = 0.0
        
        # إستهلال قيمة مجموع الخطأ
        self.error_sum_ = 0.0
        
        # إستهلال القيمة المستهدفة بصفر
        self.set_point_ = 0
        # إستهلال قيمة الزمن البدائي
        self.start_time_ = start_time

        # حفظ القيمة السابقة للزمن
        self.last_timestamp_ = 0.0

        # تخزين قيم جهد التحكم
        self.u_p = [0]
        self.u_d = [0]

    # تحديد الإرتفاع المستهدف
    def setTarget(self, target):
        self.set_point_ = float(target)

    # تحديد قيمة معامل تحكم التناسب
    def setKP(self, kp):        
        self.kp_ = float(kp)
    
    # تحديد قيمة معامل تحكم التفاضل
    def setKD(self, kd):       
        self.kd_ = float(kd)

    # تحديث
    def update(self, measured_value, timestamp):
        # حساب معامل التغير في الزمن
        delta_time = timestamp - self.last_timestamp_
        
        if delta_time == 0:
            # لو كانت دلتا الوقت تساوي صفر
            return 0
        
        # حساب الخطأ كناتج الفرق بين القيمة المستهدفة
        # و القيمة المحسوبة        
        error = self.set_point_ - measured_value

        # تحديث قيمة الزمن السابق بالزمن الحالي 
        self.last_timestamp_ = timestamp
        
        # حساب مجموع الخطأ 
        self.error_sum_ += error * delta_time
        
        # حساب التغير في الخطأ
        delta_error = error - self.last_error_
        
        #تحديت الخطأ الأخير بالخطأ الحالي
        self.last_error_ = error
        
        # حساب خطأ التناسب
        p = self.kp_ * error
        
        # حساب خطأ التفاضل
        d = self.kd_ * (delta_error / delta_time)
        
        
        # تحديد جهد التحكم
        u = p + d
        
        # تخزين قيم جهد التحكم 
        self.u_p.append(p)
        self.u_d.append(d)

        return u

المحاكاة

# معامل التناسب
kp = 0.76
# ومعامل التكامل
ki = 0.10
# معايير المحاكاة
N = 500 # عدد نقاط المحاكاة
t0 = 0  # وقت البداية
tf = 30 # وقت النهاية
time = np.linspace(t0, tf, N)
dt = time[1] - time[0] # التغير في الزمن

##################
# إستهلال القيم
y = [0, 0]
   #y[0] = قيمة الإرتفاع
   #y[1] = قيمة السرعة

# إستهلال مصفوفة لتخزين القيم
soln = np.zeros((len(time),len(y)))

# قيمة متخكم التناسب
pi = PI_Controller()

# تحديد معامل التناسب
pi.setKP(kp)

# تحديد معامل التكامل
pi.setKP(kp)

# تحديد قيمة الإرتفاع
r = 10 # أمتار
pi.setTarget(r)

# محاكاة حركة الطائرة
j = 0 # عداد
for t in time:
    # جساب الحالة في النفطة التالية للزمن
    y = ydot(y,t,pi)
    # تخزين النتائج
    soln[j,:] = y
    j += 1

# رسم النتائج
SP = np.ones_like(time)*r 
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax1.plot(time, soln[:,0],time,SP,'--')
ax1.set_xlabel('Time, (sec)')
ax1.set_ylabel('Altitude, (m)')

ax2 = fig.add_subplot(212)
ax2.plot(time, soln[:,1])
ax2.set_xlabel('Time, (sec)')
ax2.set_ylabel('Speed, (m/s)')
plt.tight_layout()
plt.show()

fig2 = plt.figure()
ax3 = fig2.add_subplot(111)
ax3.plot(time, p.u_p, label='u_p', linewidth=3, color = 'red')
ax3.set_xlabel('Time, (sec)')
ax3.set_ylabel('Control Effort')
h, l = ax3.get_legend_handles_labels()
ax3.legend(h, l)
plt.tight_layout()
plt.show()
##################
y0 = soln[:,0] #الإرتفاع
rise_time_index =  np.argmax(y0&gt;r)
RT = time[rise_time_index]
print("The rise time is {0:.3f} seconds".format(RT))

OS = (np.max(y0) - r)/r*100
if OS < 0:
    OS = 0
print("The percent overshoot is {0:.1f}%".format(OS))

print ("The steady state offset at 30 seconds is {0:.3f} meters".format(abs(soln[-1,0]-r)))

والرسومات الناتجة هي

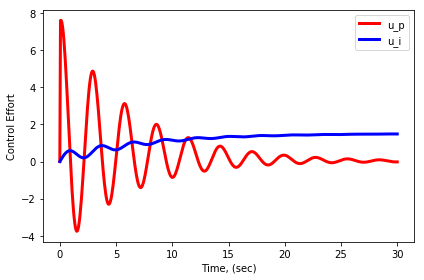
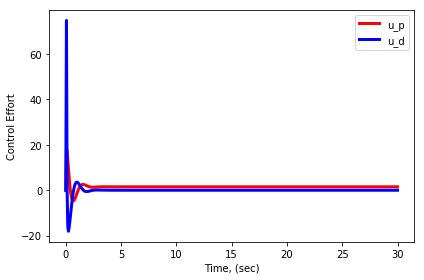
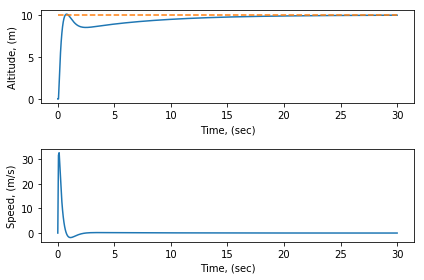
السرعة بالنسبة للزمن و الإرتفاع بالنسبة للزمن

متحكم التناسب و التفاضل :

مع إضافة التكامل تمكننا من تقليل خطأ الإستقرار ، ولكن هذا حدث على حساب زمن الإستجابة و نسبة تجاوز الهدف. و لكن التفاضل بوسعه محاولة التنبؤ بمقدار الخطأ عن طريق محاولة النظر في القيم المستقبلية وذلك بإستقراء (Extrapolation ) التغير في قيمة الخطأ و بالأخذ في عين الإعتبار هذا التغير فالنظام سيصل إلى نقطة الهدف بشكل إنسيابي و سلس.

$f^{\prime}\left(x_{k}\right) \approx \frac{f\left(x_{k}\right)-f\left(x_{k-1}\right)}{\Delta t} \Rightarrow \frac{e_{k}-e_{k-1}}{\Delta t}$

برمجة المتحكم

معادلات حركة الطائرة

#  نفس الكود السابق

متحكم التناسب والتكامل

class PI_Controller:
    def __init__(self, kp = 0.0, ki = 0.0, start_time = 0):
        
        # إستهلال القيمة الأوليه لمعامل متحكم التناسب
        # ومعامل متحكم التفاضل
        self.kp_ = float(kp)
        self.kd_ = float(kd)
        
        #إستهلال قيمة الخطأ الأخير
        self.last_error_ = 0.0
        
        # إستهلال قيمة مجموع الخطأ
        self.error_sum_ = 0.0
        
        # إستهلال القيمة المستهدفة بصفر
        self.set_point_ = 0
        # إستهلال قيمة الزمن البدائي
        self.start_time_ = start_time

        # حفظ القيمة السابقة للزمن
        self.last_timestamp_ = 0.0

        # تخزين قيم جهد التحكم
        self.u_p = [0]
        self.u_d = [0]

    # تحديد الإرتفاع المستهدف
    def setTarget(self, target):
        self.set_point_ = float(target)

    # تحديد قيمة معامل تحكم التناسب
    def setKP(self, kp):        
        self.kp_ = float(kp)
    
    # تحديد قيمة معامل تحكم التفاضل
    def setKD(self, kd):       
        self.kd_ = float(kd)

    # تحديث
    def update(self, measured_value, timestamp):
        # حساب معامل التغير في الزمن
        delta_time = timestamp - self.last_timestamp_
        
        if delta_time == 0:
            # لو كانت دلتا الوقت تساوي صفر
            return 0
        
        # حساب الخطأ كناتج الفرق بين القيمة المستهدفة
        # و القيمة المحسوبة        
        error = self.set_point_ - measured_value

        # تحديث قيمة الزمن السابق بالزمن الحالي 
        self.last_timestamp_ = timestamp
        
        # حساب مجموع الخطأ 
        self.error_sum_ += error * delta_time
        
        # حساب التغير في الخطأ
        delta_error = error - self.last_error_
        
        #تحديت الخطأ الأخير بالخطأ الحالي
        self.last_error_ = error
        
        # حساب خطأ التناسب
        p = self.kp_ * error
        
        # حساب خطأ التفاضل
        d = self.kd_ * (delta_error / delta_time)
        
        
        # تحديد جهد التحكم
        u = p + d
        
        # تخزين قيم جهد التحكم 
        self.u_p.append(p)
        self.u_d.append(d)

        return u

المحاكاة

# معامل التناسب
kp = 0.76
# ومعامل التكامل
ki = 0.10
# معايير المحاكاة
N = 500 # عدد نقاط المحاكاة
t0 = 0  # وقت البداية
tf = 30 # وقت النهاية
time = np.linspace(t0, tf, N)
dt = time[1] - time[0] # التغير في الزمن

##################
# إستهلال القيم
y = [0, 0]
   #y[0] = قيمة الإرتفاع
   #y[1] = قيمة السرعة

# إستهلال مصفوفة لتخزين القيم
soln = np.zeros((len(time),len(y)))

# قيمة متخكم التناسب
pi = PI_Controller()

# تحديد معامل التناسب
pi.setKP(kp)

# تحديد معامل التكامل
pi.setKP(kp)

# تحديد قيمة الإرتفاع
r = 10 # أمتار
pi.setTarget(r)

# محاكاة حركة الطائرة
j = 0 # عداد
for t in time:
    # جساب الحالة في النفطة التالية للزمن
    y = ydot(y,t,pi)
    # تخزين النتائج
    soln[j,:] = y
    j += 1

# رسم النتائج
SP = np.ones_like(time)*r 
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax1.plot(time, soln[:,0],time,SP,'--')
ax1.set_xlabel('Time, (sec)')
ax1.set_ylabel('Altitude, (m)')

ax2 = fig.add_subplot(212)
ax2.plot(time, soln[:,1])
ax2.set_xlabel('Time, (sec)')
ax2.set_ylabel('Speed, (m/s)')
plt.tight_layout()
plt.show()

fig2 = plt.figure()
ax3 = fig2.add_subplot(111)
ax3.plot(time, p.u_p, label='u_p', linewidth=3, color = 'red')
ax3.set_xlabel('Time, (sec)')
ax3.set_ylabel('Control Effort')
h, l = ax3.get_legend_handles_labels()
ax3.legend(h, l)
plt.tight_layout()
plt.show()
##################
y0 = soln[:,0] #الإرتفاع
rise_time_index =  np.argmax(y0&gt;r)
RT = time[rise_time_index]
print("The rise time is {0:.3f} seconds".format(RT))

OS = (np.max(y0) - r)/r*100
if OS < 0:
    OS = 0
print("The percent overshoot is {0:.1f}%".format(OS))

print ("The steady state offset at 30 seconds is {0:.3f} meters".format(abs(soln[-1,0]-r)))

الناتج

الإرتفاع بالنسبة للزمن و السرعة بالنسبة للزمن

متحكم التناسب و التكامل و التفاضل :

برمجة هذه المتحكم تكون بإضافة جميع الأكواد السابقة لبعضها كالأتي :

معادلات حركة الطائرة

#  نفس الكود السابق

متحكم التناسب والتكامل

class PI_Controller:
    def __init__(self, kp = 0.0, ki = 0.0, start_time = 0):
        
        # إستهلال القيمة الأوليه لمعامل متحكم التناسب
        # ومعامل متحكم التفاضل
        self.kp_ = float(kp)
        self.kd_ = float(kd)
        
        #إستهلال قيمة الخطأ الأخير
        self.last_error_ = 0.0
        
        # إستهلال قيمة مجموع الخطأ
        self.error_sum_ = 0.0
        
        # إستهلال القيمة المستهدفة بصفر
        self.set_point_ = 0
        # إستهلال قيمة الزمن البدائي
        self.start_time_ = start_time

        # حفظ القيمة السابقة للزمن
        self.last_timestamp_ = 0.0

        # تخزين قيم جهد التحكم
        self.u_p = [0]
        self.u_d = [0]

    # تحديد الإرتفاع المستهدف
    def setTarget(self, target):
        self.set_point_ = float(target)

    # تحديد قيمة معامل تحكم التناسب
    def setKP(self, kp):        
        self.kp_ = float(kp)
    
    # تحديد قيمة معامل تحكم التفاضل
    def setKD(self, kd):       
        self.kd_ = float(kd)

    # تحديث
    def update(self, measured_value, timestamp):
        # حساب معامل التغير في الزمن
        delta_time = timestamp - self.last_timestamp_
        
        if delta_time == 0:
            # لو كانت دلتا الوقت تساوي صفر
            return 0
        
        # حساب الخطأ كناتج الفرق بين القيمة المستهدفة
        # و القيمة المحسوبة        
        error = self.set_point_ - measured_value

        # تحديث قيمة الزمن السابق بالزمن الحالي 
        self.last_timestamp_ = timestamp
        
        # حساب مجموع الخطأ 
        self.error_sum_ += error * delta_time
        
        # حساب التغير في الخطأ
        delta_error = error - self.last_error_
        
        #تحديت الخطأ الأخير بالخطأ الحالي
        self.last_error_ = error
        
        # حساب خطأ التناسب
        p = self.kp_ * error
        
        # حساب خطأ التفاضل
        d = self.kd_ * (delta_error / delta_time)
        
        
        # تحديد جهد التحكم
        u = p + d
        
        # تخزين قيم جهد التحكم 
        self.u_p.append(p)
        self.u_d.append(d)

        return u

المحاكاة

# معامل التناسب
kp = 0.76
# ومعامل التكامل
ki = 0.10
# معايير المحاكاة
N = 500 # عدد نقاط المحاكاة
t0 = 0  # وقت البداية
tf = 30 # وقت النهاية
time = np.linspace(t0, tf, N)
dt = time[1] - time[0] # التغير في الزمن

##################
# إستهلال القيم
y = [0, 0]
   #y[0] = قيمة الإرتفاع
   #y[1] = قيمة السرعة

# إستهلال مصفوفة لتخزين القيم
soln = np.zeros((len(time),len(y)))

# قيمة متخكم التناسب
pi = PI_Controller()

# تحديد معامل التناسب
pi.setKP(kp)

# تحديد معامل التكامل
pi.setKP(kp)

# تحديد قيمة الإرتفاع
r = 10 # أمتار
pi.setTarget(r)

# محاكاة حركة الطائرة
j = 0 # عداد
for t in time:
    # جساب الحالة في النفطة التالية للزمن
    y = ydot(y,t,pi)
    # تخزين النتائج
    soln[j,:] = y
    j += 1

# رسم النتائج
SP = np.ones_like(time)*r 
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax1.plot(time, soln[:,0],time,SP,'--')
ax1.set_xlabel('Time, (sec)')
ax1.set_ylabel('Altitude, (m)')

ax2 = fig.add_subplot(212)
ax2.plot(time, soln[:,1])
ax2.set_xlabel('Time, (sec)')
ax2.set_ylabel('Speed, (m/s)')
plt.tight_layout()
plt.show()

fig2 = plt.figure()
ax3 = fig2.add_subplot(111)
ax3.plot(time, p.u_p, label='u_p', linewidth=3, color = 'red')
ax3.set_xlabel('Time, (sec)')
ax3.set_ylabel('Control Effort')
h, l = ax3.get_legend_handles_labels()
ax3.legend(h, l)
plt.tight_layout()
plt.show()
##################
y0 = soln[:,0] #الإرتفاع
rise_time_index =  np.argmax(y0&gt;r)
RT = time[rise_time_index]
print("The rise time is {0:.3f} seconds".format(RT))

OS = (np.max(y0) - r)/r*100
if OS < 0:
    OS = 0
print("The percent overshoot is {0:.1f}%".format(OS))

print ("The steady state offset at 30 seconds is {0:.3f} meters".format(abs(soln[-1,0]-r)))

و الرسومات الناتجة كما يلي :

ملخص متحكم البيد :

فلنراجع ما تعلمناه حتى الأن عن متحكم البيد و تأثير كل معايير. مدخل المتحكم هو مجموع المعايير الثلاثة التناسب التكامل التفاضل.

$u(t)=K_{p} e(t)+K_{i} \int_{0}^{t} e(\tau) d \tau+K_{d} \frac{d e(t)}{d t}$

متحكم التناسب

خطأ التناسب يأخذ في عين الإعتبار الحاضر فقط ، أي قيمة الخطا الحالي فقط . بينما زيادة معييار التناسب يقوم بإنقاص زمن الصعود (rise time) و لكنه يقوم أيضا بزيادة حدة تردد الذبذبات (frequency of oscillations) وزيادة قيمة تجاوز الهدف (overshoot) و بالتالي متحكم التناسب لوحده فشل في جعل النظام يصل إلى حالة إستقرار .

متحكم التكامل

متحكم التكامل قام بجمع قيم كل الأخطاء السابقة و هذا ما ساعده في إيصال النظام لحالة إستقرار لكنه أدى إلى زيادة حدة تردد الذبذبات و وزيادة زمن الإستقرار كذلك.

متحكم التفاضل

متحكم التفاضل لا يؤثر على إستقرار النظام و لكنه يحاول أن يتنبأ كيف سيتغير الخطأ في المستقبل ، وهو يتأثر كثيراً بالضوضاء لكنه يساعد في تقليل وقت الإستقرار و تقليل قيمة تجاوز الهدف

الجدول التالي يلخص ما تحدثنا عنه

المعييار	زمن الصعود	تجاوز الهدف	زمن الإستقرار	خطأ حالة الإستقرار
Kp	ينقص	يزيد	تغيير طفيف	ينقص
Ki	ينقص	يزيد	يزيد	يتخلص منه
Kd	تغيير طفيف	ينقص	ينقص	لا يؤثر نظرياً

نقاط ضعف متحكم البيد

كما ذكرنا فمتحكم البيد منتشر بشكل كبير في الصناعه لرخص تصنيعه و سهولة إستخدامه حيث لا تتطلب فهم للنموذج الرياضي (mathematical model) للعملية المراد التحكم بها.

لكن أحد نقاط ضعف متحكم البيد هو انه يتفاعل فقط مع الإضطرابات التي تحدث في النظام ، بمعنى أن النظام لابد أن يشعر بوجود خطأ قبل أن يقوم المتحكم بتصحيحه .

و نقطة أخرى هي أنه لا يتعامل بشكل جيد مع الأنظمة ذات زمن ميت (dead time) أو تاخر (lag) عالي

و الزمن الميت هو الوقت المستغرق من اللحظة التي يرسل في المتحكم إشارة إلى اللحظة التي يستقبل فيها النظام هذه الإشارة ويبدأ في التفاعل.

ذكرنا بأن أغلب متحكمات البيد هي في الواقع متحكم PI فgماذا لا يستخدم معييار التفاضل ، السبب في ذلك هو تأثره الكبير بالضوضاء كمثال لو كان لدينا طائرة رباعية (quadrotor) و كانت تحلق في إرتفاعها المرغوب به . لكن الرياح كانت قوية في ذلك اليوم لذلك الطائرة تتأرجح للأعلى و الأسفل ، معادلة معييار التفاضل هي كالأتي .

$\frac{d e}{d t} \approx \frac{\left(e-e_{o l d}\right)}{\Delta t}$

قيمة دلتا تي صغيرة جداً و تكاد تصل إلى أجزاء من الثانية ، و بالطبع القسمة على رقم صغير تساوي الضرب على قيمة كبيرة جداً و الناتج سيكون عدد كبير . و عملياً هذا الأمر سيحدث مشكلة كبيرة لأن المتحكم يعتقد بأن هناك تغيير كبير وبالتالي سيستجيب بالمثل.

يمكن إضافة مٌرشح منخفض التردد (low pass filter) لإزالة بعض الضوضاء عالية التردد (high frequency noise,) لكن هذا سيؤدي تقليل جودة أداء متحكم التفاضل لأنه يعتمد على الإستجابة لأي تغيير في الهواء .

غالباً هذا يتطلب مقدار كبير من الإختبارات للوصول إلى توازن بين الضوضاء و بين الأداء المرغوب. تطبيق بسيط لمرشح منخفض التردد هو المرشح التكراري من الدرجة الأولى (first order recursive filter)

$\bar{D}[k]=\alpha \frac{(k]-e[k-1]}{\Delta t}+(1-\alpha) \bar{D}[k-1], \alpha \epsilon[0,1]$

ألفا هي عامل التنعيم (smoothing factor) كلما قللنا الألفا سيزداد مقدار الضوضاء التي سنتخلص منها ، وهذا يعني إضافة معييار أخر لابد من إختياره من قبل مصمم المتحكم بالإضافة إلى ذلك فالمرشح التكراري سيؤدي إلى حدوث تأخر (lag) و هذا سيؤدي إلى تأخر وصول إشارة المتحكم إلى النظام مما يُصعب التحكم بالنظام

أهداف و مقاييس تصميم المتحكمات

الإستقرار : أنظمة التحكم من الضروري أن تؤدي إلى إستقرار النظام . في الواقع هناك عدة طرق للتعريف إحداها هي بيبو (BIBO) و التي تشمل الأنظمة الخطية وتنص على أن طالما أن المُدخل تحت قيمة معينة فالمُخرج كذلك سيكون تحت قيمة مُعينة. و تعريف أشمل هو ما يعرف بالإستقرار المُقارب (ُ asymptotic stability) و مفاده أن النظام سيصل حتما لحالة إستقرار إذا تم إعطاءه مُدخل محدد أو شرط إبتدائي . كمثال إذا رمينا كرة من علو ما ، فالكرة حتما ستسقر على الأرض.

التتبع : تتبع الأداء مهم أيضا ، و نقصد هنا قدرة نظام التحكم في المحافظة على الإشارة المرجعية حيث أن الفرق بين الإشارة المرجعية و المُخرج هي خطأ التتبع. كمثال على ذلك الثرموستات في أجهزة التكييف .

قوة التحمل : يُفضل أن لا يكون نظام التحكم مبني على نموذج رياضي مُفصل مع معايير ذات درجة عالية من الدقة ، على العكس يفضل أن يكون النظام مرن وصالح للعمل على نطاق واسع من المعايير المختلفة

الإضطرابات : جميع أنظمة التحكم معرضة للضوضاء و الإضطرابات و الأخطاء القياسية ، و رغم أنه من المهم محاولة تقليل هذه الإضطرابات فالمهم أيضاً محاولة تصميم أنظمة تحكم تتحمل هذه الإضطرابات .

الطريقة المتبعه في تصميم أنظمة التحكم :

تحديد مواصفات أداء النظام كمثال تقليل زمن الذروة أو زمن الإستقرار…..إلخ
تطوير نموذج رياضي بسيط للنظام
إختيار الحساسات و نوع التحكم
تصميم التحكم ليلائم مواصفات الأداء
لو كان ممكن فبوسعنا إستخدام المحاكاة لإختبار أداء التحكم
إختيار البرامج أو الأجهزة التي سنطبق التحكم عليها
مؤالفة التحكم .

إستراتيجيات المؤالفة :

في السابق كانت تستخدم إستراتيجيتين تسميان (Z-N methods) و لفترة طويلة كانتا معايير الصناعة و يمكنكم قراءة المزيد عنهما هنا و هنا

http://engineering.ju.edu.jo/Laboratories/07-PID%20Controller.pdf

https://yilinmo.github.io/EE3011/Lec9.html#orge604ea4

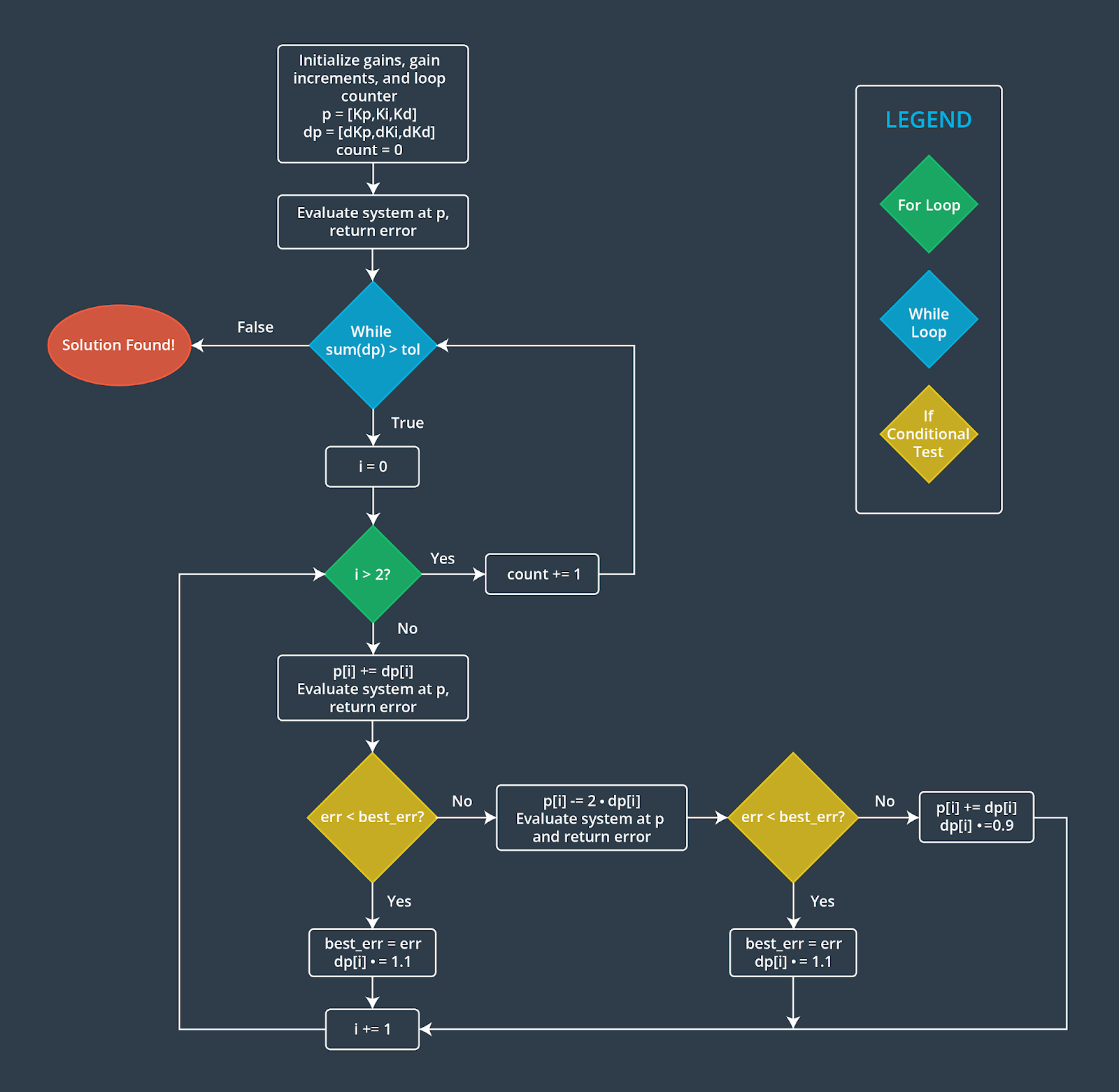
و حالياً تستخدم خوارزمية النزول الإشتقاقي (Gradient Descent Algorithm) و المعروفة أيضا بتويدل (Twiddle)

خوارزمية النزول الإشتقاقي

وهي طريقة ألية لمؤالفة التحكم . و تعمل كالأتي في البداية نقوم إستهلال قيم معاملات التحكم الثلاثة و في الغالب يُنصح بأن تكون قيمة معامل التناسب قيمة صغيره لا صفرية ، بينما معامل التكامل و معامل التفاضل كلاهما صفر. ومن ثم نغير بشكل بسيط كل القيم الثلاث بمقدار بسيط و نرى إذا كان هذا سيقلل من دالة الخسارة ( تحدث عن هذه الدالة في هذا المقال)

التحدي هنا هو إختيار ما الذي ستُركز علي دالة الخساره ، هل هو نسبة تجاوز الهدف أو زمن الإستقرار ، أو خليط من الإثنين.

و برمجة هذه الخوارزمية لتحاول قدر الإمكان تقليل نسبة تجاوز الهدف:

import numpy as np
import matplotlib.pyplot as plt

def ydot(y, t, dt, r, p):
    ''' 
    المعايير:
    -----------
    y = تحتوي على سبعة قيم
    t = الزمن بالثواني
    dt = الخطوة الزمنية
    r = النقطة المستهدقة
    p = معايير التحكم الثلاثة
    '''
    # Model states
    y1 = y[0] # الإرتفاع
    y2 = y[1] # السرعة
    y3 = y[2] # الخطأ
    y4 = y[3] # تكامل الأخطاء 
    y5 = y[4] # تحكم التناسب
    y6 = y[5] # تحكم التكامل 
    y7 = y[6] # تحكم التفاضل 

    # الخطأ الحالي للموقع
    e = r - y1

    # جهد التحكم
    Kp = p[0]
    Ki = p[1]
    Kd = p[2]
    up = Kp*e # جهد تحكم التناسب
    ui = Ki*(e*dt + y4) # جهد تحكم التكامل
    ud = Kd*(e - y3)/dt # جهد تحكم التفاضل
    u = up + ui + ud # مجمل جهد التحكم

    # الحد الأقصى للمحركات
    if u > umax:
        u = umax # المٌخرج الأقصى الممكن 
    elif u < 0:
        u = 0 # محركات الطائرة لايمكن أن تعكس
    ### حالة لإشتقاق
    # لو الإرتفاع 0
    if (y1 <= 0.):
        # لو كان جهد التحكم أقل من الجاذبية الطائرة تبقى في الأرض

        if u <= np.absolute(g*m/c):
            y1dot = 0.
            y2dot = 0.
        else:
            # لو كان الجهد أكبر من الجاذبية الطائرة تندفع للأعلى 
            y1dot = y2
            y2dot = g + c/m*u - 0.75*y2 #NOTE: I added damping to make the system easier to control
    else: # وإلا فإن الطائرة محلقة في الجو
        y1dot = y2
        y2dot = g + c/m*u - 0.75*y2 #NOTE: I added damping to make the system easier to control

    # حساب الحالة الجديدة
    y1 += y1dot*dt
    y2 += y2dot*dt
    y3 = e
    y4 += e*dt
    y5 = up
    y6 = ui
    y7 = ud
    return [y1, y2, y3, y4, y5, y6, y7]

def hover(p):
    ''' 
        هذه الدالة تحاكي حركة الطائرة كإستجابة
        للتغير في النقطة المستهدفة للإرتفاع
        
    '''
    # إستهلال القيم
    y = [0, 0, 0, 0, 0, 0, 0]
    soln = np.zeros((len(time),len(y)))

    j = 0 
    for t in time:
        y = ydot(y,t,dt,r,p)
        soln[j,:] = y
        j += 1
    return soln

def cost_fun(soln):
    '''
    دالة الخسارة تحاول تقليل
    قيمة تجاوز الهدف
    '''
    y0 = soln[:,0] #الإرتفاع
    rise_time_index =  np.argmax(y0>r)
    RT = time[rise_time_index]

    OS = (np.max(y0) - r)/r*100
    OS_pen = OS
    if OS < 0:
        OS = 0
        OS_pen = 100
    
    return OS_pen**2

def twiddle(tol=0.05):
    p = [2, 2, 2]
    dp = [0.10, 0.10, 0.10]
    soln = hover(p)
    best_cost = cost_fun(soln)
    it = 0
    while sum(dp) > tol:
        print("Iteration {}, best error = {}".format(it, best_cost))
        for i in range(len(p)):
            p[i] += dp[i]
            # Can't have negative gains
            if p[i] < 0:
                p[i] = 0
            soln = hover(p)
            cost = cost_fun(soln)

            if cost < best_cost:
                best_cost = cost
                dp[i] *= 1.1
            else:
                p[i] -= 2 * dp[i]
        
                if p[i] < 0:
                    p[i] = 0
                soln = hover(p)
                cost = cost_fun(soln)

                if cost < best_cost:
                    best_cost = cost
                    dp[i] *= 1.1
                else:
                    p[i] += dp[i]
            
                    if p[i] < 0:
                        p[i] = 0
                    dp[i] *= 0.9
        it += 1
    return p


# معايير المحاكاة
N = 500 # عدد نقاط المحاكاة
t0 = 0  # وقت البداية
tf = 30 # وقت النهاية
time = np.linspace(t0, tf, N)
dt = time[1] - time[0] # delta t, (sec)
r = 10 # التغير في الزمن

# معاملات النموذج
g = -9.81 # الجاذبية
m =  1.54 # وزن الطائرة
c = 10.   # ثابت معدل الإرسال الكهروميكانيك
umax = 5.0 #مُخرج التحكم الأقصى

p = twiddle()
print(p)
soln = hover(p)

# رسم النتائج
SP = np.ones_like(time)*r 
UMAX = np.ones_like(time)*umax
fig = plt.figure()
ax1 = fig.add_subplot(311)
ax1.plot(time, soln[:,0],time,SP,'--')
ax1.set_xlabel('Time, (sec)')
ax1.set_ylabel('Altitude, (m)')
ax2 = fig.add_subplot(312)
ax2.plot(time, soln[:,1])
ax2.set_xlabel('Time, (sec)')
ax2.set_ylabel('Speed, (m/s)')

fig2 = plt.figure()
ax3 = fig2.add_subplot(111)
ax3.plot(time, soln[:,4], '-r', label="Up")
ax3.plot(time, soln[:,5], '-b', label="Ui")
ax3.plot(time, UMAX,'--k', label="Umax")
ax3.set_xlabel('Time, (sec)')
ax3.set_ylabel('Cont. Effort, (m/s/s)')
ax3.legend(loc='upper left')
plt.tight_layout()
plt.show()

و الرسومات الناتجة للموالفة كالتالي :

و بهذا نكون قد وصلنا إلى ختام هذا المقال. في حال رغبتكم في تجريب أي من الأكواد التي قمنا بإستخدامها فتجدونها على الكولاب

مقدمة في أنظمة التحكم

أنظمة التحكم المفتوحة العقدة

أنظمة التحكم المغلقة العقدة

التحكم التناسبي التكاملي التفاضلي

المحاكاة :

متحكم التناسب :

متحكم التناسب و التكامل :

متحكم التناسب و التفاضل :

متحكم التناسب و التكامل و التفاضل :

ملخص متحكم البيد :

متحكم التناسب

متحكم التكامل

متحكم التفاضل

نقاط ضعف متحكم البيد

أهداف و مقاييس تصميم المتحكمات

الطريقة المتبعه في تصميم أنظمة التحكم :

إستراتيجيات المؤالفة :

خوارزمية النزول الإشتقاقي

إضافة تعليق

إلغاء التعليق

تحليل معادلات الحركة لروبوت Kuka KR210

التصنيفات

أخر المقالات

نمط التصميم : المدخلات متعدد الوسائط

من الإجراءات إلى النتائج: تعلم كيفية التبسيط

معالجة اللغة الطبيعة في الرعاية الصحية

معالجة اللغة الطبيعية في تويتر

نمذجة الموضوع

أنماط تصميم تمثيل البيانات: السمة المتقاطعة

أنظمة التوصية للبيانات النصية

أنماط تصميم تمثيل البيانات : التضمينات

تلخيص النص

إنضم إلى النشرة البريدية

الوصول السريع

مقدمة في أنظمة التحكم

أنظمة التحكم المفتوحة العقدة

أنظمة التحكم المغلقة العقدة

التحكم التناسبي التكاملي التفاضلي

المحاكاة :

متحكم التناسب :

متحكم التناسب و التكامل :

متحكم التناسب و التفاضل :

متحكم التناسب و التكامل و التفاضل :

ملخص متحكم البيد :

متحكم التناسب

متحكم التكامل

متحكم التفاضل

نقاط ضعف متحكم البيد

أهداف و مقاييس تصميم المتحكمات

الطريقة المتبعه في تصميم أنظمة التحكم :

إستراتيجيات المؤالفة :

خوارزمية النزول الإشتقاقي

إضافة تعليق

قد يعجبك أيضاً

التصنيفات

أخر المقالات

إنضم إلى النشرة البريدية

الوصول السريع