
في هذا المشروع سنقوم ببرمجة معادلات الحركة الأمامية (Forward Kinematics) و معادلات الحركة العكسية (Inverse Kinematics) ليد روبوت مصممة لعمليات الإلتقاط و الوضع (pick and place) تعرف بأسم يد كوكا (KUKA KR210) و يتكون الروبوت من ستة أضلاع و ستة مفاصل . من إجل تطبيق و إختبار خوارزميات معادلات الحركة تم إستخدام كل من روس (ROS) و غازيبوا (Gazebo ) و ارفيز (rviz ).
في معادلات الحركة الأمامية سنقوم بتقدير موضع مقبض اليد (gripper) بإستخدام زوايا الأضلاع (links angles) المكون منها الروبوت . بينما في معادلات الحركة العكسية سيتم إعطائنا قائمة لوضعيات مختلفة لمقبض يد الروبوت منها سنقوم بحساب زاويا المفاصل (joint angles ) التي تربط أضلاع الروبوت .
بالنظر لتركيب اليد يلاحظ أن المفاصل الأخيرة الثلاثة للروبوت هي دائرية (revolute) و محاور المفصل تتقاطع جميعها في نقطة واحدة فلدينا ما يسمى بالمعصم الكروي (spherical wrist) و يعتبر المعصم الخامس هو نقطة التقاطع ولذلك يسمى مركز المعصم (wrist center). وهذا ما يمنحنا القدرة على فصل معادلات الحركة العكسية إلى جزئين وهما معادلات الدوران العكسي (inverse Orientation) و معادلات الموضع العكسية (Inverse Position) .
ولذلك سنقوم أولاً بحل معادلات الموضع العكسية بما أنه لدينا معصم كروي يربط المفاصل 4 و 5 و 6 فموضع مركز المعصم في الفضاء الثلاثي الأبعاد يحدده المفاصل الثلاثة الأولى . و بالتالي فيمكننا تحديد موضع مركز المعصم بإستخدام مصفوفات التحويل التي سنقوم بحسابها بناءً على موضع مقبض اليد . للعلم فالهدف من المفاصل الثلاثة الأخيرة هي منح مقبض اليد دقة عالية لتأدية وظيفتها .
هدفنا الأول هو تجهيز بييئة العمل و من ثم تشغيل المشروع في بيئته الإقتراضية في وضعية العرض (demo mode) حتى نحصل على صورة كاملة للمشروع . وبعد ذلك معاينة معادلات الحركة الأمامية ليد كوكا حتى نتعرف على هيكل الروبوت و حساب معايير دي إتش (DH parameters)
تجهيز بيئة العمل :
قمت بإستخدام البيئة التالية للعمل على المشروع :
- Ubuntu 16.04 LTS OS
- ROS Kinetic 1.12.12
- Gazebo 7.9
- RVIZ version 1.12.15
بعد تنصيب روس على نظام أوبنتو سنقوم ببناء مساحة العمل و تحميل ملفات المشروع كالأتي :
- بناء مساحة العمل
$ mkdir -p ~/catkin_ws/src $ cd ~/catkin_ws/ $ catkin_make
- تحميل ملفات المشروع
$ cd ~/catkin_ws/src $ git clone https://github.com/udacity/RoboND-Kinematics-Project.git
- تنصيب التبعيات الناقصة
$ cd ~/catkin_ws $ rosdep install --from-paths src --ignore-src --rosdistro=kinetic -y
- تغيير أذونات بعض السكربت لنجعلها قابلة للتنفيذ (executable)
$ cd ~/catkin_ws/src/RoboND-Kinematics-Project/kuka_arm/scripts $ sudo chmod u+x target_spawn.py $ sudo chmod u+x IK_server.py $ sudo chmod u+x safe_spawner.sh
- بناء المشروع
$ cd ~/catkin_ws $ catkin_make
- إضافة بعض الأوامر لملف الباش
$ echo "source ~/catkin_ws/devel/setup.bash" >> ~/.bashrc $ echo "export GAZEBO_MODEL_PATH=~/catkin_ws/src/RoboND-Kinematics-Project/kuka_arm/models" >> ~/.bashrc $ source ~/.bashrc
تشغيل المشروع في وضعية العرض ، للتاكد من أن كل شيئ يعمل كما يفترض.
- فتح الملف المسمى inverse_kinematics.launch و الموجود في المسار /catkin_ws/src/RoboND-Kinematics-Project/kuka_arm/launch و التاكد من أن قيمة الديمو “true”
<launch>
<node name="trajectory_sampler" pkg="kuka_arm" type="trajectory_sampler">
<!--set demo value="false" when using IK_server-->
<param name="demo" value="false" type="bool"/>
</node>
</launch>
- فتح المشروع
$ cd ~/catkin_ws/src/RoboND-Kinematics-Project/kuka_arm/scripts/ $ ./safe_spawner.sh
عندما يفتح كل من غازيبوا و أرفيز فسيظهر لنا الأتي :
ومن هناك يمكننا الضغط على التالي (next) ورؤية المشروع
في حالة رغبتا في إستخدام تحليلنا للمعادلات الحركة سنستخدم الأمر التالي في نافذة جديدة
$ rosrun kuka_arm IK_server.py
تحليل معادلات الحركة الأمامية
1- تعريف معايير دي إتش (DH Parameters) :
سنستخدم ترميز دينافيت هارتنبيرغ (Denavit-Hartenberg ) لحساب معاييرنا
- طول الأضلاع (link lengths) من (d1-d7)
- إزاحة الأضلاع (link offsets) من (a0 -a6)
- زوايا الإلتواء (twist angles ) من (alpha0 – alpha6)
- زوايا المفاصل (joint angles) من (q1 -q7)
و لمعرفة طريقة حساب هذه القيم يرجى مشاهدة الفيديو التالي (هنا)
و بإختصار يتم حسابها كالأتي :
- d(i) – طول الضلع (الحالي) : المسافة من المفصل السابق إلى المفصل الحالي على طول محور الصاد (z-axis)
- a(i-1) – إزاحة الضلع (السابق) : المسافة من المفصل السابق إلى المفصل الحالي على طول محور السين (x-axis)
- alpha(i-1) – زاوية الإلتواء (السابقة) : الزاوية بين محور الصاد السابق و محور الصاد الحالي .
- q(i) – زاوية المفصل (الحالية) : زاوية دوران المفصل الحالية حول محور الصاد الحالي
الوضعية الصفرية أو وضعية الراحة ليد كوكا من داخل أرفيز كما في الصورة التالي
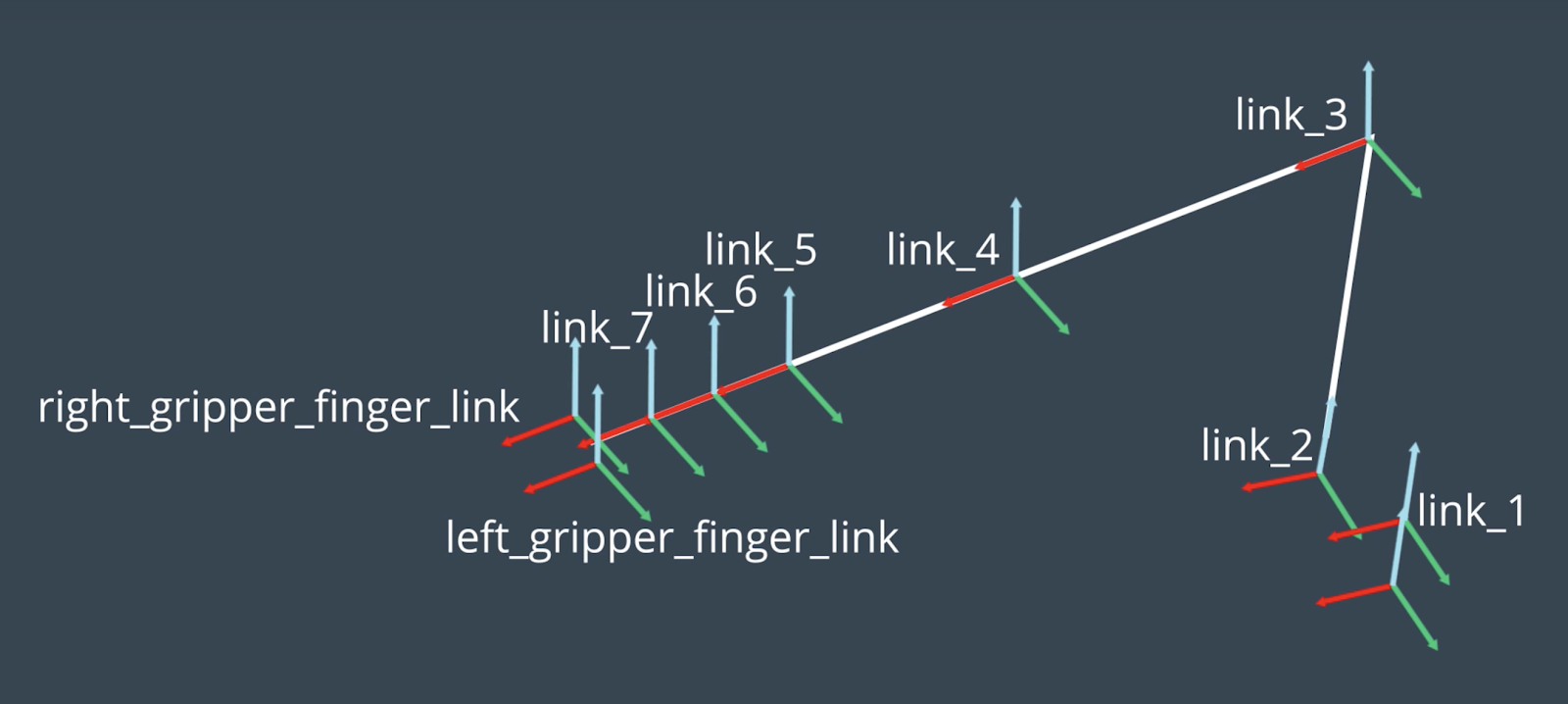
ومحاور اليد مُعطاة كما في الصورة الأتية
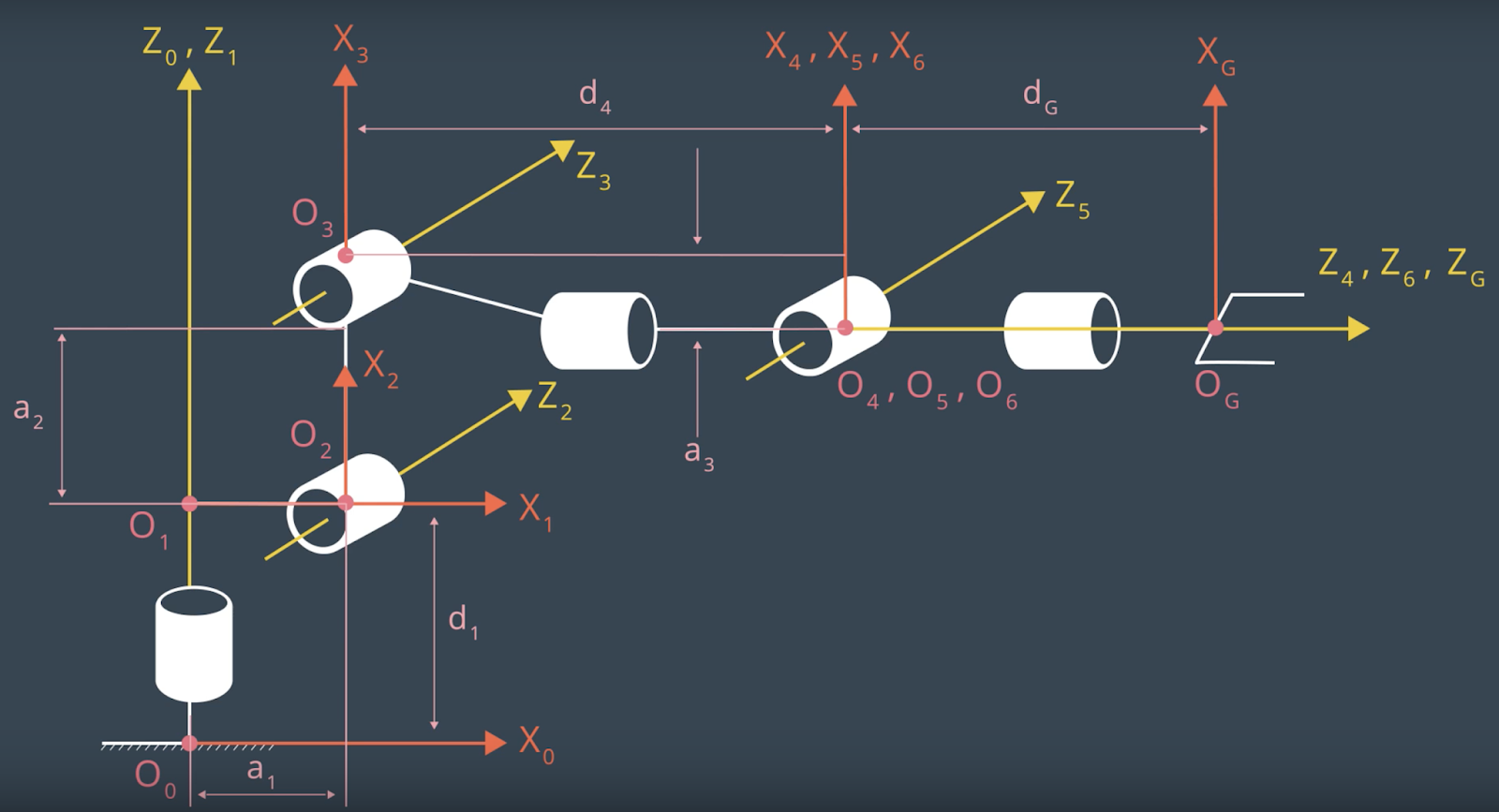
وزوايا الإلتواء معطاة في الجدول االأتي
| الزاوية | المحور الأول | المحور الثاني | الإستدارة | قيمة الزاوية |
| α0 | z0 | Z1 | موازي | 0 |
| α1 | Z1 | Z2 | عمودي | -90 |
| α2 | Z2 | Z3 | موازي | 0 |
| α3 | Z3 | Z4 | عمودي | -90 |
| α4 | Z4 | Z5 | عمودي | 90 |
| α5 | Z5 | Z6 | عمودي | -90 |
| α6 | Z6 | Zg | موازي | 0 |
ويمكن معرفة قيم أطوال الإضلاع و قيم الإزاحة من ملف URDF الموجود في المسار
/catkin_ws/src/RoboND-Kinematics-Project/kuka_arm/urdf
و هذا جزء من الكود داخل الملف
<!-- joints -->
<joint name="fixed_base_joint" type="fixed">
<parent link="base_footprint"/>
<child link="base_link"/>
<origin xyz="0 0 0" rpy="0 0 0"/>
</joint>
<joint name="joint_1" type="revolute">
<origin xyz="0 0 0.33" rpy="0 0 0"/>
<parent link="base_link"/>
<child link="link_1"/>
<axis xyz="0 0 1"/>
<limit lower="${-185*deg}" upper="${185*deg}" effort="300" velocity="${123*deg}"/>
</joint>
ما يهمنا هنا هو الموجود في خانة origin و بعد كتابة هذه الملف في جدول نحصل على التالي :
| O | joint | parent | child | x | y | z | r | p | y |
|---|---|---|---|---|---|---|---|---|---|
| 0 | fixed_base | base_footprint | base_link | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | joint_1 | base_link | link_1 | 0 | 0 | 0.33 | 0 | 0 | 0 |
| 2 | joint_2 | link_1 | link_2 | 0 .35 | 0 | 0.42 | 0 | 0 | 0 |
| 3 | joint_3 | link_2 | link_3 | 0 | 0 | 1.25 | 0 | 0 | 0 |
| 4 | joint_4 | link_3 | link_4 | 0.96 | 0 | -0.054 | 0 | 0 | 0 |
| 5 | joint_5 | link_4 | link_5 | 0.54 | 0 | 0 | 0 | 0 | 0 |
| 6 | joint_6 | link_5 | link_6 | 0.193 | 0 | 0 | 0 | 0 | 0 |
| 7 | gripper | link_6 | gripper_link | 0.11 | 0 | 0 | 0 | 0 | 0 |
| . | Total (m) | 2.153 | 0 | 1.946 | 0 | 0 | 0 |
و بالإستعانه بالجدول السابق يمكننا رسم المحاور المختلفة و تحديد قيم التنقل بين كل محور و الأخر حول محوري السين (x-axis) و الصاد (z-axis)
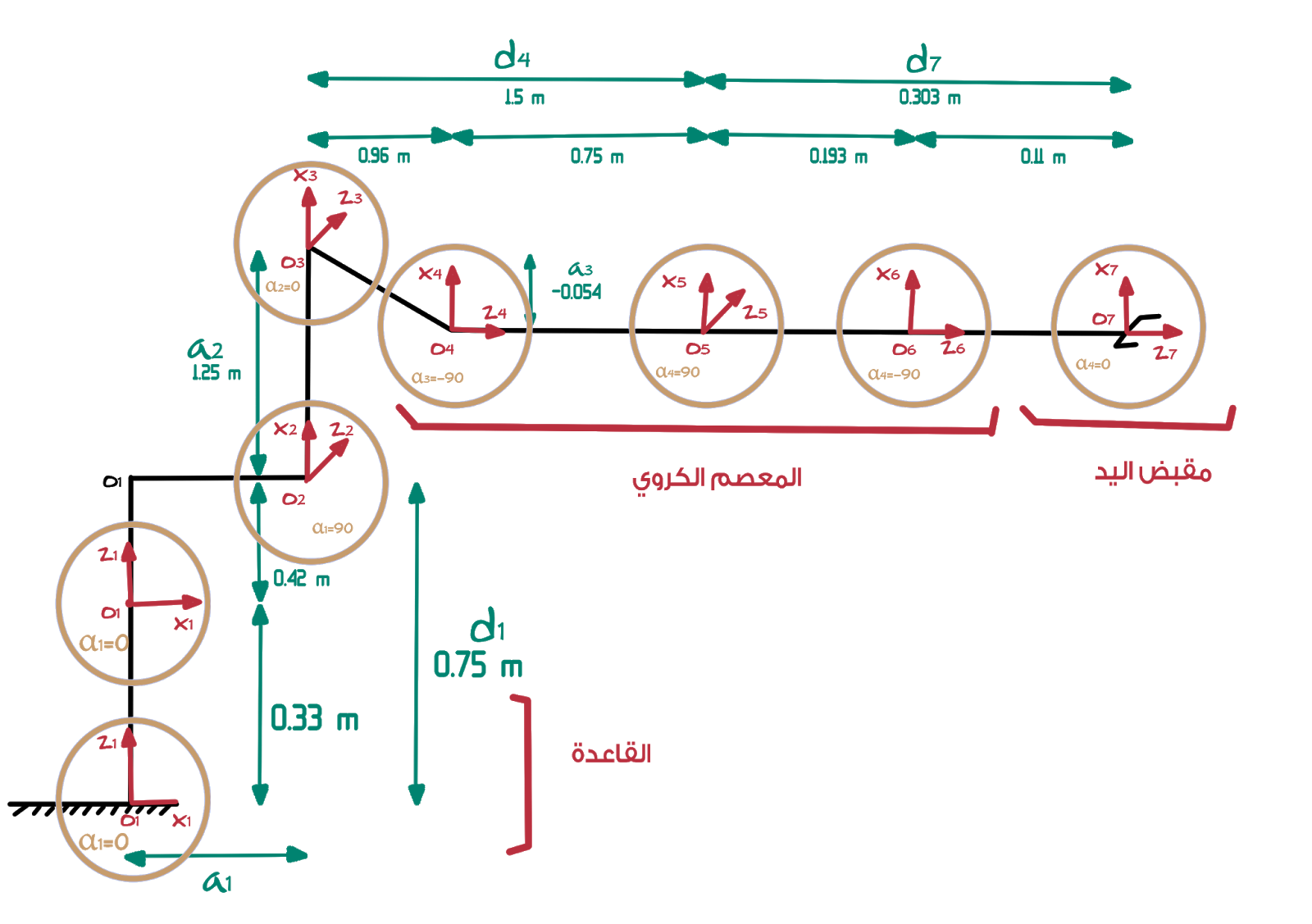
و يمكن تبسيط هذا أكثر عن طريق جمع المفاصل الثلاثة الأخيرة (4 و 5 و 6 ) في المفصل الخامس بما أنه يمثل مركز المعصم
و هذا الجدول يمثل قيم معايير دي إتش
| الأضلاع | i | alpha(i-1) | a(i-1) | d(i) | theta(i) |
|---|---|---|---|---|---|
| 0->1 | 1 | 0 | 0 | 0.75 | q1 |
| 1->2 | 2 | – pi/2 | 0.35 | 0 | -pi/2 + q2 |
| 2->3 | 3 | 0 | 1.25 | 0 | q3 |
| 3->4 | 4 | – pi/2 | -0.054 | 1.5 | q4 |
| 4->5 | 5 | pi/2 | 0 | 0 | q5 |
| 5->6 | 6 | – pi/2 | 0 | 0 | q6 |
| 6->EE | 7 | 0 | 0 | 0.303 | 0 |
و يمكن برمجة هذا الجدول كالأتي
DH_TABLE = {alpha0: 0, a0: 0, d1: 0.75, q1: q1,
alpha1: -pi/2, a1: 0.35, d2: 0, q2: -pi/2+q2,
alpha2: 0, a2: 1.25, d3: 0, q3: q3,
alpha3: -pi/2, a3: -0.054, d4: 1.5, q4: q4,
alpha4: pi/2, a4: 0, d5: 0, q5: q5,
alpha5: -pi/2, a5: 0, d6: 0, q6: q6,
alpha6: 0, a6: 0, d7: 0.303, q7: 0}
2- حساب مصفوفة التحويل المتجانس ( Homogeneous Transformation)
مصفوفة التحويل المتجانس تحتوي كل من عناصر الدوران و التنقل بين مفاصل الروبوت ، ويمكن حسابها بإستخدام معادلة دي إتش الأتية :
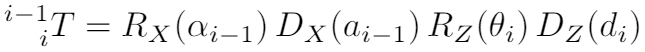
و عند تعويض كل من مصفوفي الإتجاه و الدوران (rotation and orientation ) فستأخذ المصفوفة المتجانسة هذه الهيئة :
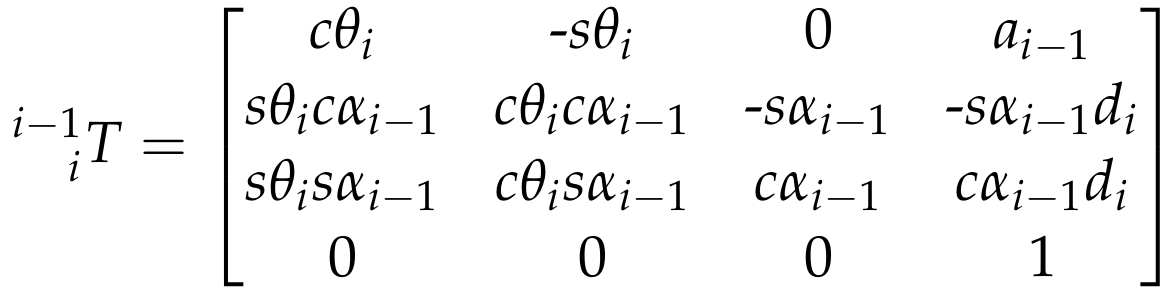
و عند برمجتها نستخدم دالة لحساب هذه المصفوفات التحويل
def TF_MATRIX(alpha, a, theta, q):
TF_MAT = Matrix([
[ cos(q), -sin(q), 0, a],
[sin(q)*cos(alpha), cos(q)*cos(alpha), -sin(alpha), -sin(alpha)*d],
[sin(q)*sin(alpha), cos(q)*sin(alpha), cos(alpha), cos(alpha)*d],
[ 0, 0, 0, 1]])
return TF_MAT
2.1 – حساب مصفوفات التحويل (Transformation matrix )
و يتم حساب مصفوفات التحويل الفردية بهذه الطريقة :
T0_1 = TF_MATRIX(alpha0, a0, d1, q1).subs(DH_TABLE) T1_2 = TF_MATRIX(alpha1, a1, d2, q2).subs(DH_TABLE) T2_3 = TF_MATRIX(alpha2, a2, d3, q3).subs(DH_TABLE) ...
و بعض تعويض معايير DH في الدالة السابقة سنحصل على مصفوفات التحويل الأتية
2.2 – مصفوفات التحويل المركبة (Compositions of the transformation matrices)
يمكن الحصول على مصفوفات التحويل المركبة عن ضرب المصفوفات في الترتيب المرغوب به
T0_2 = T0_1 * T1_2 # القاعدة للضلع 2 T0_3 = T0_2 * T2_3 # القاعدة للضلع 3 T0_4 = T0_3 * T3_4 # القاعدة للضلع 4 T0_5 = T0_4 * T4_5 # القاعدة للضلع 5 T0_6 = T0_5 * T5_6 # القاعدة للضلع 6
2.3 – حساب موضع و دوران مقبض اليد نسبة إلى قاعدة الربوت (T0_grip)
سنحصل على ذلك عن طريق ضرب كل المصفوفات ببعضها.
T0_grip = T0_1 * T1_2 * T2_3 * T3_4 * T4_5 * T5_6 * T6_grip
2.4 – إستخراج تحويل الدوران ( rotation transformation ) من القاعدة إلى المفصل 3
يمكن الحصول على دوران المفصل الثالث نسبة إلى القاعدة من عناصر الدوران في مصفوفة التحويل المركبة كالأتي
R0_3 = T0_1[0:3, 0:3] * T1_2[0:3, 0:3] * T2_3[0:3, 0:3]
2.5 – حساب تحويل الدوران العكسي (inverse rotation transformation ) من المفصل الثالث إلى القاعدة
بما أن مصفوفة الدوران متماثلة (symmetric) فمقلوبها (inverse ) يساوي المنقول (transpose )
R3_0 = R0_3.transpose()
تحليل معادلات الحركة العكسية (Inverse Kinematic Analysis) :
عندما نعطي الروبوت أمر ، فنحن نعطيه موضع الجسم المطلوب حمله و دوران مقبض اليد المطلوب لمسك الجسم . ولذلك في المحاكاة عندما نحن نحدد موضع الجسم في ملف (spawn_location ) فسنحصل على متجهات الموضع (pose vector) و التي تحتوي موقع ودوران مقبض اليد المطلوب للوصول للجسم .
# موقع مقبض اليد px = req.poses[i].position.x py = req.poses[i].position.y pz = req.poses[i].position.z # زوايا الدوران رباعية الأبعاد oa = req.poses[i].orientation.x ob = req.poses[i].orientation.y oc = req.poses[i].orientation.z od = req.poses[i].orientation.w
سنحصل على زوايا الدوران من المحاكاة على شكل مًتجهة رباعية و بالتالي نحن في حاجة تحويلها إلى زوايا الدوران الثلاث الإنحدار (pitch) و الإنعراج (yaw) و الإلتفات (roll )
شاهد هذه الفيديو لمعلومات أكثر https://www.youtube.com/watch?v=pQ24NtnaLl8
ولعمل ذلك فسنستخدم الدالة euler_from_quaternion() لتحويل الزوايا إلى صيغة أويلر (euler representation)
# تحويل الزوايا من رباعية الإبعاد إلى زوايا أويلر # (roll, pitch, yaw) = دوران مقبض اليد (roll, pitch, yaw) = tf.transformations.euler_from_quaternion([oa, ob, oc, od]) pos = [px, py, pz] ori = [roll, pitch, yaw]
1- التحويل من معايير urdf معايير دي إتش
كما نعلم فالنظام الإحداثي المستخدم في المحكاة هو urdf و حتى نقوم بإجراء حساباتنا فعلينا أن نحول هذه الإحداثيات إلى النظام الإحداثي لدي إتش ، و في روبوت كوكا هناك إختلاف بين دوران المقبض المُعرف في URDF و دوران المقبض في تحليلنا السابق لمعايير دي إتش.
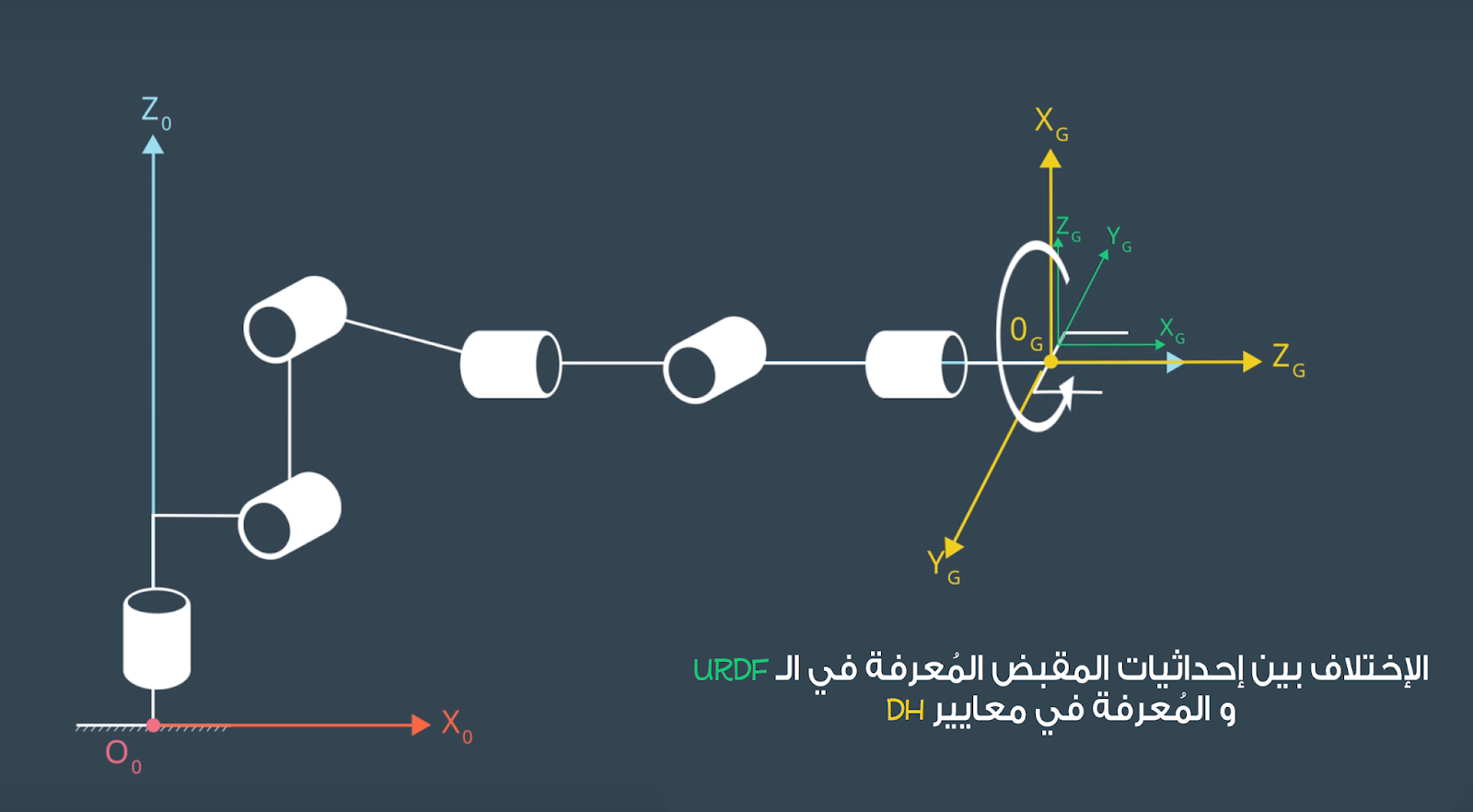
و حتى نراعي هذا الإختلاف سنقوم بحساب الدوران الداخلي (intrinsic rotation) و سمي بذلك لأن محاور الدوران ليست ثابته بل تتغير بدوران الجسم و نقوم بذلك بإستخدام هذه المعادلة
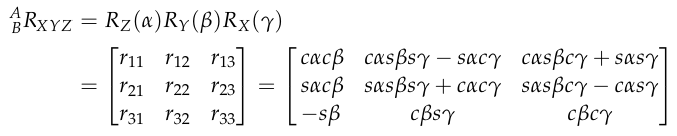
و نستخدم هذه الدالة في عملية برمجة هذا التحويل
def URDF2DH(r, p ,y):
URDF2DH_ROT_X = Matrix([
[ 1, 0, 0],
[ 0, cos(r), -sin(r)],
[ 0, sin(r), cos(r)]])
URDF2DH_ROT_y = Matrix([
[ cos(p), 0, sin(p)],
[ 0, 1, 0],
[-sin(p), 0, cos(p)]])
URDF2DH_ROT_z = Matrix([
[ cos(y),-sin(y), 0],
[ sin(y), cos(y), 0],
[ 0, 0, 1]])
return URDF2DH_ROT_X , URDF2DH_ROT_y , URDF2DH_ROT_z
r, p ,y = symbols('r p y')
rot_x, rot_y, rot_z = URDF2DH(r, p, y)
و إحداثيات مقبض اليد يمكن تحويلها من الهيكل الإحداثي (frame axis ) في نظام urdf إلى نظام دي إتش عن طريق تدوير مقبض اليد 180 درجة في المحور العيني (z-axis ) و -90 درجة في المحور الصادي (y-axis) و بالتالي يمكن الحصور على الإحداثيات الصحيح للمقبض في وضعية الراحة كالأتي :
URDF2DH_grip_rot_correction = rot_z.subs(y, pi) * rot_y.subs(p, -pi/2)
و من ثم إجراء عملية الدوران الداخلي(intrinsic rotation) عندما يكون دوران مقبض اليد في وضعية عشوائية كالأتي :
# الحصول على موقع و دوران المقبض من المحاكاة
grip = Matrix(pos)
ori = Matrix(ori)
rot_grip = rot_Z * rot_y * rot_x
rot_grip = rot_grip * URDF2DH_grip_rot_correction
rot_grip = rot_grip.subs({'r': ori[0], 'p': ori[1], 'y': ori[2]}
و بما أن ضلع مقبض اليد على المحور الصادي (Z-axis) مطابق (coincident ) للضلع السادس (Link-6) فبالتالي الدوران من الضلع السادس إلى المقبض يساوي مصفوفة المطابقة (identity matrix) مما يعني أن الدوران من القاعده إلى المقبض يساوي الدوران من القاعدة إلى الضلع السادس . و بما أن مقبض اليد يبعد مسافة (d7) من مركز المعصم (wrist center ) أي المفصل الخامس (join-5) . فيمكن حساب موضع مركز المعصم نسبة إلى القاعدة كالأتي :
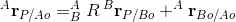
كما يمكن الحصول على مركز المعصم نسبة للقاعده عن طريق ضرب هاتين المصفوفتين و طرح مسافة المقبض من المركز من ناتج الضرب
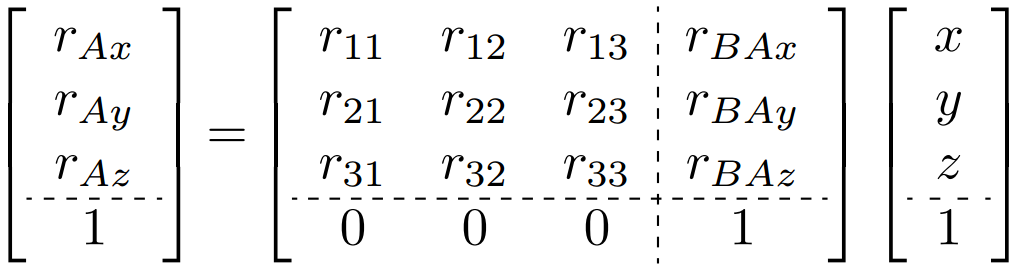
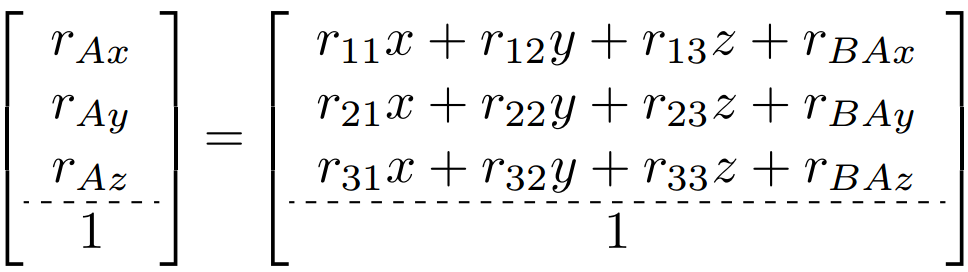
و يمكننا برمجة هذه العملية بالشكل الأني :
R0_6 = rot_grip
grip2WC_Translation = Matrix([
[0],
[0],
[DH_TABLE[d7]]])
WC = grip - R0_6*grip2WC_Translation
2- حساب ثيتا 1 و ثيتا 2 و ثيتا 3 :
حتى هذه اللحظة فالمشروع كان في غاية السهولة ، كل شيئ عبارة عن تعويض مباشر و لكن هنا كانت نقطة التحول بالنسبة لي و إنتقل هذا المشروع من شيئ خفبف و مرح إلى تحدي حقيقي فحساب المثلثات هي فعليا نقطة ضعفي ، فإستمتعت في هذه الجزئية .
لحساب الثيتا سنستخدم موقع مركز المعصم (wrist-center) وقيم معايير دي إتش . سنقوم في البداية بحساب قيم الثيتا 1 و الثيتا 2 و ثيتا 3 .
الزاوية ثيتا 1: هي الزاوية في مستوى السين و الصاد (x-y plane) الناتجة عن إسقاط مركز المعصم (wrist-center) على المستوى السيني و الصادي في النظام الإحداثي لهيكل القاعدة (base-frame coordinate system)
الزاوية ثيتا 2 : هي زاوية دوران المفصل الثاني (joint-2) من وضع الراحة حول المحور العيني الثاني (Z2 axis)
الزاوية ثيتا 3 : هي زاوية دوران المفصل الثالث (joint-3) من وضع الراحة حول المحور العيني الثالث (Z3 axis)
و هذه الصورة توضح الزوايا الثلاثه
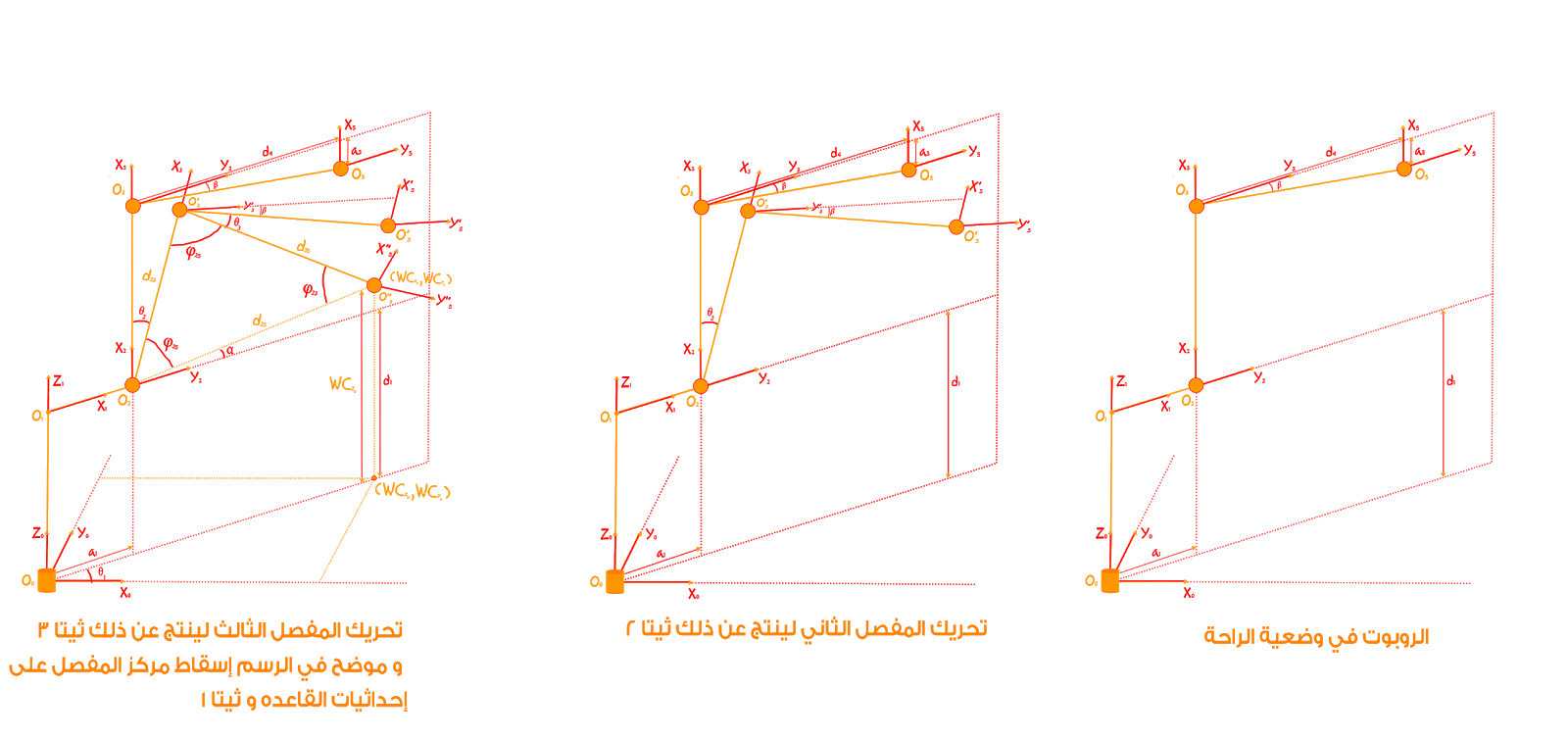
عند حساب مركز المعصم المسقط على المستوى السيني و الصادي للقاعدة أي (X0-Y0 plane) من إحداثيات هيكل القاعدة (base frame coordinates) سنقوم بالأتي :
طول المعصم هو المُكون في إتجاه (x0) مطروح منه إنزايح الضلع (link-offset) أي a1 من المفصل الثاني (joint 2)
إرتفاع المعصم هو المُكون في إتجاه (z0) مطروح منه طول الضلع (link-length) أي d1 من المفصل الثاني (joint 2)
xc = sqrt(WC[0]**2 + WC[1]**2 - DH_TABLE[a1]) yc = WC[2] - DH_TABLE[d1]
الزاوية بين المفصل الثالث و المفصل الخامس نسبة إلى تصميم الضلع في اليد هي :
beta = abs(atan2(DH_TABLE[a3], DH_TABLE[d4]))
وبين المفصل الثاني و الثالث كالأتي :
alpha = atan2(yc, xc)
بالنسبة للزاويتين ثيتا 2 و ثيتا 3 سنستخدم قانون جيب التمام (cosine law) لمثلث معلوم الأضلاع . و أضلاع المثلث في هذه الحالة هي المسافة بين المفاصل 2 و 3 و 5 مع الأخذ في الإعتبار بأن المفصلين 4 و 6 متطابقين (coincide ) مع إحداثيات المفصل الخامس . و يمكن الحصول على قيم أضلاع المثلث كالأتي :
d2_3 = DH_TABLE[a2] d3_5 = sqrt(DH_TABLE[d4]**2 + DH_TABLE[a3]**2) d2_5 = sqrt(xc**2 + yc**2)
بما أن طول أضلاع جوانب المثلت معروفة ، فيمكن حساب الزوايا قانون جيب تمام الزاوية كمثال الزاوية بين الجانب الضلع a و الضلع b يمكن إيجادها بإستخدام المعادلة
![]()
لحساب قوس جيب تمام الزاوية من قوس ظل تمام الزاوية سنستخدم المعادلة الأتي من متطابقات الدوال المثلثية العكسية
![]()
و برمجة قانون جيب التمام كالأني
cos_law = lambda a, b, c: (a**2 + b**2 - c**2) / (2 * a * b) cos_a = cos_law(d2_5, d2_3, d3_5) cos_b = cos_law(d2_3, d3_5, d2_5) cos_c = cos_law(d2_5, d3_5, d2_3) cos_inv = lambda x: atan2(sqrt(1 - x**2), x) angle_a = cos_inv(cos_a) angle_b = cos_inv(cos_b) angle_c = cos_inv(cos_c)
و بالإستعانة بالحسابات السابقة فيمكن حساب ثيتا 1 و ثيتا 2 و ثيتا 3 كالأتي :
theta1 = atan2(WC[1],WC[2]).evalf() theta2 = (pi/2 - (angle_a + alpha)).evalf() theta3 = (pi/2 - (angle_b + beta )).evalf()
3- حساب مصفوفات الدوران العكسية
بإستخدام زوايا المفاصل ثيتا فستقوم بحساب دورن مفصل القاعدة (joint-0) نسبة إلى المفصل الثالث (joint-3)
R3_0 = R3_0.evalf(subs={q1: theta1, q2:theta2, q3:theta3})
و الأن مصفوفت الدوران من المفصل الثالث إلى مقبض اليد هي :
R3_6 = R3_0 * rot_grip
و بالإستعانة بمصفوفة التحويل المتجانس (homogeneous transformation) نحن نعلم بأن عناصر المصفوفة R3_6 ، عندما تكون sin(theta-5) لا تساوي صفر هي كالأتي :
R3_6 = [[-sin(q4)*sin(q6) + cos(q4)*cos(q5)*cos(q6), -sin(q4)*cos(q6) - cos(q4)*cos(q5)*sin(q6), -cos(q4)*sin(q5)], [ sin(q5)*cos(q6), -sin(q5)*sin(q6), cos(q5)], [-sin(q4)*cos(q5)*cos(q6) - cos(q4)*sin(q6), sin(q4)*cos(q5)*sin(q6) - cos(q4)*cos(q6), sin(q4)*sin(q5)]]
و عندما تكون sin(theta-5) = 0
R3_6 = # [theta-5 = 0 or theta-5 = 2*pi] [[ cos(q4)*cos(q6), -cos(q4)*sin(q6), 0], [ 0, 0, 1], [-sin(q4)*cos(q6), sin(q4)*sin(q6), 0]] R3_6 = # [theta-5 = pi] [[-cos(q4)*cos(q6), cos(q4)*sin(q6), 0], [ 0, 0, -1], [ sin(q4)*cos(q6), -sin(q4)*sin(q6), 0]]
4- حساب ثيتا 4 و ثيتا 5 و ثيتا 6 :
و بإستخدان عناصر المصفوفة R3_6 سنحسب ثيتا 4 و ثيتا 5 و ثيتا 6
theta5 = atan2( sqrt(R3_6[0,2]**2 + R3_6[2,2]**2), R3_6[1,2] ).evalf() if (theta5 > pi) : theta4 = atan2(-R3_6[2,2], R3_6[0,2]).evalf() theta6 = atan2(R3_6[1,1], -R3_6[1,0]).evalf() else: theta4 = atan2(R3_6[2,2], -R3_6[0,2]).evalf() theta6 = atan2(-R3_6[1,1], R3_6[1,0]).evalf()
يرجى الملاحظة بأن عناصر المصفوفة R3_6 التالية (R3_6[2,2], R3_6[0,2], R3_6[1,1] , R3_6[1,0]) المستخدمة لحساب ثيتا 4 و ثيتا 6 تتغير إشارتها بناءً على إذا ما كانت ثيتا 5 في الربع الأول و الثاني أو الربع الثالث و الخامس ، و لذلك توجب مراعاة هذا الأمر و تعيير الإشارة من أجل ضمان دقة الحسابات المتعلقة بدوران مقبض اليد
النتائج :
هذا فيديو قصير يظهر حركة الروبوت في المحاكاة (هنا)
ولتحميل الكود من أو معاينته (هنا)











إضافة تعليق